«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
ОСНОВЫ БИЗНЕСА НА РЫНКЕ ЦЕННЫХ БУМАГ Учебник / Под ред. д-ра экон. наук, профессора А. Н. Асаула. - СПб.: АНО «ИПЭВ», 2008. - 207с. РАЗДЕЛ 2. ПРОФЕССИОНАЛЬНАЯ ДЕЯТЕЛЬНОСТЬ НА РЫНКЕ ЦЕННЫХ БУМАГ Глава 8. Предпринимательская деятельность на рынке ценных бумаг 8.3. Портфельное инвестирование Главная цель вложения средств - получение максимального дохода и минимизация рисков. Оптимальным способом достижения этой цели является портфельный подход к инвестированию. Инвестиционный портфель - это сформированная в определенной пропорции совокупность ценных бумаг, принадлежащих физическим или юридическим лицам. Состав инвестиционных портфелей формируется в зависимости от текущих и стратегических целей инвесторов. Существует определенный набор инвестиционных портфелей: 1. Доходные портфели. Составляются таким образом, чтобы вкладчик мог получить доход, приемлемая величина которого соответствует степени риска, допустимой для инвестора. В этот вид портфеля входят ценные бумаги, приносящие доход выше среднего уровня (облигации АО, высокодоходные акции, государственные долговые обязательства и др.). 2. Портфели роста. Могут быть сформированы с расчетом различных темпов прироста дохода - от умеренного до быстрого: - портфели умеренного роста составляются в расчете на долгосрочную перспективу и являются наименее рискованными. Состав входящих в них ценных бумаг меняется достаточно медленно; - портфели ускоренного прироста формируются за счет приобретения и постоянного обновления состава акций компаний-эмитентов, отличающихся высокой степенью риска и быстрой оборачиваемостью активов; - портфели среднего роста включают как надежные ценные бумаги, приобретаемые на относительно большой срок, так и рисковые фондовые инструменты с повышенным доходом, состав которых все время обновляется; - страховые портфели формируются под заказ отдельных инвесторов, желающих приобрести ценные бумаги какой-либо одной отрасли или региона. 3. Портфели роста и дохода. Могут быть сформированы в виде: - балансовых портфелей, состоящих из доходных обыкновенных и привилегированных акций, а также облигаций; - портфеля двойного назначения, удачно сочетающего акции двух типов (одни приносят высокий текущий доход, другие дают большой прирост капитала). 4. Портфели ценных бумаг, освобожденные от налогов. Развиты в США, где инвестиционные фонды могут формировать портфели ценных бумаг, доходы по которым в соответствии с национальным законодательством освобождены от налогов. К таким бумагам относятся муниципальные облигации, которые при высокой степени ликвидности предполагают получение небольшого дохода. Портфель ценных бумаг дает инвестору возможность получения текущего дохода; прироста собственного капитала; одновременного увеличения капитала при получении дохода; получения доходов, освобожденных от налогообложения. При формировании портфеля следует помнить, что входящие в него компоненты должны «работать» вместе, создавая принципиально новое качество инвестиций. Это возможно только при максимально широком спектре инвестирования. «Золотое» правило современного рынка - возможность выбора, диверсификация, а значит, независимость от одного источника. Источниками могут являться конкретный локальный рынок, сектор экономики или виды ценных бумаг. Если клиент не склонен рисковать, в его портфеле будут преобладать облигации - инструменты с фиксированной доходностью. Если же он ориентирован на получение максимальной прибыли и допускает определенную степень риска, ему могут быть предложены акции наиболее динамично растущих секторов экономики - нефтегазовой промышленности, компьютерной индустрии, телекоммуникаций, атомной энергетики или ВПК. Альтернативу секторальным фондам представляют региональные; при этом не обязательно ограничиваться рынками развивающихся стран: многие клиенты предпочитают ценные бумаги американских или канадских компаний, более низкая процентная ставка которых компенсируется стабильностью и предсказуемостью. Неизменно популярными остаются товарные фонды - золота, серебра или нефти, спрос на которые вряд ли кардинально изменится. Преимущество широкой продуктовой линейки заключается в возможности выбора и комбинирования. Большинство региональных и секторальных фондов - индексные. В основе философии индексного инвестирования лежит тот факт, что в долгосрочной перспективе все рынки акций растут. Их среднегодовая доходность за последние 80 лет превышает уровень инфляции и ставки по депозитам более чем в два раза. Особенность индексных фондов заключается в неравномерности рыночной динамики. Экономические и политические условия могут быть благоприятными для определенных стран и секторов, обеспечивая высокие темпы роста цен на акции конкретных компаний. Со временем конъюнктура меняется, и лидерство по доходности переходит к другой группе компаний. Индексные фонды позволяют использовать неравномерность темпов роста - осуществлять инвестирование в выбранные группы активов. Клиент, ориентированный на получение более высокого дохода и не желающий, чтобы приобретение ценных бумаг определялось индексными показателями, выбирает фонды активного управления. Здесь успех зависит от компетентности лиц, решающих, какие акции недооценены и имеют перспективу хорошего роста. Решения может принимать сам инвестор, если он считает свою квалификацию достаточной для анализа рынка ценных бумаг. Однако чаще эту задачу выполняет управляющий - эксперт банка, специализирующийся на фондах активного управления. Именно он формирует портфель клиента и определяет индивидуальную инвестиционную стратегию. При наличии определенной суммы денег и желания приобрести ценные бумаги на определенный промежуток времениинвестор сталкивается с проблемой выбора инвестиционного портфеля. Принимая решение о приобретении того или иного портфеля ценных бумаг, инвестор не располагает достаточной информацией о его доходности, он может судить только об ожидаемой или средней доходности исходя из дохода, полученного по этим ценным бумагам в прошлом. Многие инвесторы руководствуются правилом, что недооцененные ценные бумаги будут востребованы. Таким образом, проблема выбора того или иного портфеля достаточно сложна. Доходность ценных бумаг вычисляют по формуле
где CJ – будущая стоимость ценных бумаг; PV – текущая стоимость ценной бумаги и цена покупки. Если портфель состоит из определенного числа разных по стоимости ценных бумаг, доходность определяют по формуле
где rр – среднеожидаемая доходность портфеля; хi – количество ценных бумаг / вида; ri -– ожидаемая доходность ценной бумаги / вида; N – количество ценных бумаг в портфеле (1,2,3, ... N).
В 1952 г. американский экономист, лауреат Нобелевской премии в области экономики Гарри Марковщ опубликовал работу об инвестировании с точки зрения теории формирования портфеля ценных бумаг Согласно его теории, для принятия решения о вложении средств инвестору не нужно проводить оценку всех портфелей, достаточно рассмотреть лишь так называемое эффективное множество портфелей. Теорема об эффективном множестве гласит: инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает: - максимальную ожидаемую доходность для некоторого уровня риска; - минимальный риск для некоторого значения ожидаемой доходности. При этом Марковиц утверждает, что при обосновании портфеля инвестор должен руководствоваться ожидаемой доходностью и стандартным отклонением: - ожидаемая доходность является мерой потенциального вознаграждения, связанной с конкретным портфелем; - стандартное отклонение - мера риска, связанная с данным портфелем. С помощью метода, предложенного Г. Марковицем, можно сформировать большое количество портфелей ценных бумаг, часть из которых будет относиться к эффективному множеству. Для выделения оптимальных портфелей Марковиц использовал алгоритм квадратического программирования (метод критических линий). Нахождение оптимального портфеля с помощью указанного алгоритма включает ряд процедур: - рассмотрение портфелей, доступных инвестору; - нахождение структуры ценных бумаг каждого из бесконечного множества портфелей; - оценку вектора ожидаемых доходностей и ковариационной матрицы; - определение количества угловых портфелей. Под угловым понимается портфель, обладающий такими свойствами, что любая комбинация двух смежных угловых портфелей представляет третий портфель, лежащий в эффективном множестве между этими двумя угловыми портфелями; - выбор оптимального портфеля. Обозначив ожидаемую доходность оптимального портфеля r* а ожидаемые доходности двух ближайших угловых портфелей - соответственно ra и rh, то состав оптимального портфеля можно рассчитать по формуле
Оптимальный портфель будет состоять из доли у, инвестированной в ближайший угловой портфель, находящийся выше оптимального, и доли 1 - у, инвестированной в ближайший угловой портфель, расположенный ниже оптимального. Следовательно, предложенный Г. Марковицем подход ориентирован на то, что инвестор имеет некоторый начальный капитал, который он может полностью использовать для формирования портфелей с определенным риском. При этом оптимальный портфель идентифицируется с точкой касания кривых безразличия инвестора с эффективным множеством, характеризуемым не только определенной доходностью, но и риском. Модель Марковича используют при формировании оптимального портфеля ценных бумаг на российском рынке. Для метода определения доходности инвестиционного портфеля используют ковариацию и корреляцию. Ковариация - это статистическая мера взаимодействия двух случайных переменных, в качестве которых в нашем случае выступают доходности двух ценных бумаг (i и j). Экономический смысл положительного взаимодействия состоит в том, что рост ожидаемой доходности одной ценной бумаги влечет за собой увеличение доходности другой. Отрицательная ковариация показывает, что рост ожидаемой доходности одной ценной бумаги сопровождается снижением ожидаемой доходности другой. Положительная ковариация получается, если портфель сформирован из акций компаний разных отраслей. Ковариацию используют при расчете стандартного отклонения портфеля. Стандартное отклонение Gp портфеля, состоящего из двух ценных бумаг (i и j), рассчитывают по формуле
где N – количество ценных бумаг в портфеле; Gij – ковариация доходности ценных бумаг i и j; Gp – стандартное отклонение. Ковариация весьма близка по смыслу к корреляции. Корреляция - это взаимосвязь случайных переменных. Для ее измерения используют коэффициент корреляции, который всегда находится в интервале -1...+1. Если р = -1, это означает полную отрицательную корреляцию, если р = +1 - полную положительную корреляцию. Коэффициент корреляции нормирует ковариацию для облегчения сравнения с другими парами переменных. Ковариация двух случайных переменных равна
где GiGj – стандартное отклонение соответственно i и j ценной бумаги.
С помощью данного уравнения можно показать, что коэффициент корреляции между ценными бумагами i и j равен
При анализе стандартного отклонения производят двойное суммирование: анализ произведения весов двух ценных бумаг Хi Хj и ковариации этих двух ценных бумаг в определенной последовательности. Любой ковариационной матрице соответствует корреляционная матрица, которая может быть определена по данным ковариационной матрицы и уравнению корреляции. Портфель, в состав которого входят несколько видов ценных бумаг, выбрать нетрудно. Если же формируется портфель из сотен или тысячи ценных бумаг, возникает проблема выбора из эффективного множества портфелей, представляющих собой оптимальную комбинацию доходности и стандартного отклонения, а также предпочтений инвестора относительно риска и доходности. Существует несколько моделей, используемых для формирования портфелей ценных бумаг. Если доходность обыкновенной акции за данный период связана с индексом РТС, то с ростом рыночного индекса, вероятно, будет расти и цена акции, а с его падением цена акции будет падать. Эту взаимосвязь отражает рыночная модель (market model)
где: ri – доходность ценной бумаги; rj -доходность на рыночный индекс j за этот же период; aij – коэффициент смещения;
Как следует из данного уравнения, чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги, а Разность между действительным и ожидаемым значениями объясняется случайной погрешностью. Поэтому Коэффициент наклона в рыночной модели называют бета-коэффициентом. Он показывает отношение ценной бумаги к ее доходности.
где – Ценные бумаги, имеющие бета-коэффициент больше 1, т. е. обладающие большей изменчивостью, чем рыночный индекс, называют агрессивными, а ценные бумаги с коэффициентом меньше 1 - оборонительными. Общий риск ценной бумаги и общий риск портфеля ценных бумаг измеряют с помощью дисперсии. Общий риск ценной бумаги (у2j) будет
где
Зная о весе каждой дисконтированной ценной бумаги в портфеле и рыночном индексе, а также о долях инвестирования в каждую бумагу, доходность портфеля можно рассчитать по формуле:
где Хi = 1,2,3…,N. Подставив значение г в указанное уравнение, получим:
где
Общий риск портфеля, измеряемый дисперсией его доходности (
где
Если же случайные отклонения доходности ценных бумаг являются некоррелируемыми, т. е. не связанными между собой, то получим:
Следовательно, общий риск портфеля состоит из общего риска отдельных ценных бумаг, включающего собственный риск ( Собственный (несистематический) риск портфеля связан с тем, что некоторые из находящихся в портфеле ценных бумаг могут как возрасти, так и упасть в цене. Следовательно, практически в любом портфеле будут ценные бумаги, которые могут одинаково влиять на его доходность. Весомый вклад в определение максимальных портфелей ценных бумаг внесли Джеймс Тобин и Уильям Шарп. Они развили подход Марковица в ситуации, когда в экономике существует безрисковый актив с некоторой доходностью. Под безрисковым понимается актив, доходность от которого является определенной. Поскольку неопределенность конечной стоимости безрискового актива отсутствует, следовательно, стандартное отклонение для него равно нулю. Если безрисковый актив имеет заранее известную доходность, то ценные бумаги, входящие в актив, должны обеспечивать инвестору фиксированный доход. В этой связи вряд ли корпоративные ценные бумаги могут принести инвестору фиксированный доход. В России до недавнего времени только один тип ценных бумаг можно было отнести к безрисковым - это облигации Федерального сберегательного займа. Инвестирование в безрисковый актив иногда называют безрисковым кредитованием. Дж. Тобин показал, что, если р = (рi ..., рп) - некоторый портфель (р - для i-го актива в портфеле), a f - безрисковый актив, то все портфели вида Новую эффективную границу, полученную с учетом безрискового актива называют рыночной линией (CML, Capital Market Line), а точку 0* - рыночным портфелем (market portfolio). Уильям Шарп показал, что рыночный портфель можно вычислить из условия равенства спроса и предложения финансовых активов, рассматривая рынок как совокупность всех инвесторов и всех ценных бумаг (активов). В этом случае доля р акций типа i в портфеле 0* просто равна доле всех акций типа i на рынке. Поэтому 0* и называют рыночным портфелем. Множество оптимальных (по Марковицу - Тобину) портфелей ведет себя достаточно стабильно и меняется скачкообразно, только в моменты резких скачков котировок некоторых ценных бумаг. В эти моменты следует пересмотреть структуру портфеля. Алгоритм Марковица - Тобина дает решение задачи составления оптимального портфеля. Однако, когда исследуют очень большое количество акций, он нереализуем из-за сложности вычислений (нужно обращать матрицу огромного размера). Эдвин Элтон, Мартин Грубер и Манфред Падберг предложили свой алгоритм вычисления портфеля 0* в предположении, что набор рассматриваемых активов можно описать моделью с одним индексом. В моделях с одним индексом рассматривается рыночный индекс I, характеризующий поведение фондового рынка в целом. За границей очень популярен индекс Доу-Джонса, на нашем фондовом рынке - индекс РТС. Для рассматриваемого (базового) индекса I вводят естественное понятие доходности:
где PV0 – значение индекса в начале исследуемого периода; Сi – значение индекса в конце рассматриваемого периода.
В рамках модели с одним индексом предполагается, что доходности рассматриваемых активов представляются в виде:
bi – коэффициент наклона, вычисляемый по формуле:
аi – коэффициент смещения, определяемый по формуле:
В основе этих алгоритмов лежит предположение, что каждый инвестор стремится увеличить доходность своего портфеля без увеличения возможного риска. Для этого инвестор составляет арбитражный портфель, используя модель с одним индексом. Арбитраж - получение безрисковой прибыли путем использования разных цен на ценные бумаги. Инвесторы стремятся получить доходы при каждой возможности: продавая бумаги по высокой цене и одновременно приобретая такие же ценные бумаги по относительно низкой цене. Для реализации арбитражного подхода, как правило, применяют факторный анализ курса ценных бумаг. При этом предполагают, что можно увеличить доходность портфеля без увеличения риска. Однако ряд систематических факторов, влияющих на риск и доходность ценной бумаги, препятствует широкому применению модели APT на практике. Арбитражным называют любой портфель А = (А1, А2,... An). Для составления портфеля А не требуется дополнительных ресурсов, арбитражный портфель не чувствителен к базовому фактору и ожидается положительная доходность портфеля А. Арбитражный портфель формируется так, чтобы риск был намного меньше риска текущего портфеля. Желательно, чтобы этот риск был близок к 0. Стратегию формирования арбитражного портфеля используют при расчете оптимального портфеля ценных бумаг на российском фондовом рынке. Формирование портфеля государственных облигаций осуществляется путем покупки облигаций на аукционах, при первичном размещении или на вторичных торгах. Для покупки облигаций инвестор составляет заявку-поручение дилеру, указывая возможные цены покупки, количество бумаги и сумму денежных средств, которую он предполагает затратить. В заявке на аукцион указывают два вида покупок: - неконкурентные заявки (выполняются по средневзвешенной цене аукциона). Облигации, включенные в неконкурентные заявки, оговариваются в документах, публикуемых в официальных финансовых изданиях за 7 дней до проведения аукциона; - конкурентные заявки (удовлетворяются по цене, указанной инвестором, но не ниже цены отсечения). Цену отсечения рассчитывают организаторы аукциона на основе анализа всех участвующих в аукционе заявок. При этом инвестору важно указать цену покупки, которую он может установить путем изучения спроса. Если инвестор укажет в заявке неприемлемую для организаторов аукциона цену, заявка не будет удовлетворена. Сумму денежных средств, которую инвестор предполагает получить при размещении портфеля облигаций, рассчитывают по формуле
где С(t) – будущая сумма получения; PV – текущая сумма вложения; rа – ставка доходности, % (ставка дисконтировании).
Цену облигации при неизменных во времени ставках определяют по формуле
где Р – цена i облигации; N – номинал i облигации; rа – ставка дисконтирования; п – показатель кратности срока обращения облигации относительно базового периода. Ставку дисконтирования рассчитывают по формуле
где Ra – ставка дисконтирования;
Если изменяются условия инвестирования, то для каждого периода вложений (к примеру, месяца) можно отдельно ввести ставки дисконтирования. Тогда цену облигации можно определить так:
где Еа1,... Еап – ставки дисконтирования каждого месяца инвестиционного периода. |
||
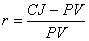
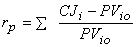
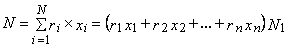
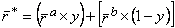
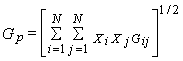
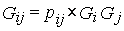
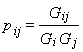
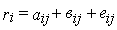
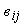 – коэффициент наклона;
– коэффициент наклона; 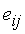 – случайная погрешность.
– случайная погрешность.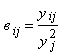
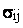 ковариация между доходностью акции i и доходностью акции рыночного индекса;
ковариация между доходностью акции i и доходностью акции рыночного индекса; 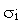 – дисперсия доходности индекса или риск ценной бумаги.
– дисперсия доходности индекса или риск ценной бумаги.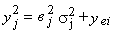
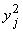 – дисперсия доходности рыночного индекса;
– дисперсия доходности рыночного индекса;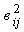
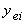 – собственный риск i ценной бумаги, мерой которого является дисперсия случайной погрешности (
– собственный риск i ценной бумаги, мерой которого является дисперсия случайной погрешности (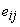 ).
).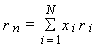
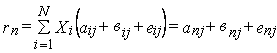
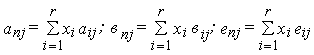
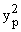 ), можно определить по формуле:
), можно определить по формуле: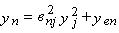
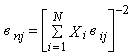
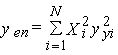
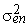 ), которого, по утверждению Г. Марковица, нельзя избежать, и рыночный риск (
), которого, по утверждению Г. Марковица, нельзя избежать, и рыночный риск (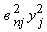 ).
).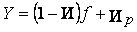 лежат на рыночной прямой, проходящей через точки 0i rf, и уp rр.Среди всех таких прямых нужно выбрать самую крутую (более крутая дает большую доходность при заданном рискер), которая проходит через точку (0, rp ) и точку касания 0* к эффективной границе.
лежат на рыночной прямой, проходящей через точки 0i rf, и уp rр.Среди всех таких прямых нужно выбрать самую крутую (более крутая дает большую доходность при заданном рискер), которая проходит через точку (0, rp ) и точку касания 0* к эффективной границе.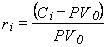
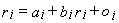
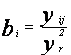
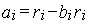
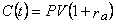
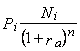
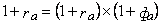
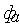 – дополнительная ставка, компенсирующая риск.
– дополнительная ставка, компенсирующая риск.