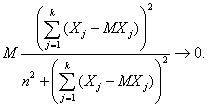«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
М.: МЗ-Пресс, 2004. П-1. Законы больших чисел Законы больших чисел позволяют описать поведение сумм случайных величин. Простейшим примерами является следующая теорема Чебышева для пространства элементарных событий из конечного числа элементов. Теорема Чебышёва. Пусть случайные величины Х1, Х2,…, Хk попарно независимы и существует число С такое, что дисперсии всех этих случайных величин не превосходят С, т.е. D(Xi)<C при всех i = 1, 2, …, k. Тогда для любого положительного ε выполнено неравенство
Частным случаем теоремы Чебышева является теорема Бернулли – первый в истории вариант закона больших чисел. Теорема Бернулли. Пусть m – число наступлений события А в k независимых (попарно) испытаниях, и р есть вероятность наступления события А в каждом из испытаний. Тогда при любом
Ясно, что при росте k выражения в правых частях формул (1) и (2) стремятся к 0. Таким образом, среднее арифметическое попарно независимых случайных величин сближается со средним арифметическим их математических ожиданий. Напомним, что до сих пор речь шла лишь о пространствах элементарных событий из конечного числа элементов. Однако приведенные теоремы верны и в общем случае, для произвольных пространств элементарных событий. Однако в условие закона больших чисел необходимо добавить требование существования дисперсий. Легко видеть, что если существуют дисперсии, то существуют и математические ожидания. Закон больших чисел в форме Чебышёва приобретает следующий вид. Теорема Чебышева [2, с.147]. Если Х1, Х2,…, Хk ,… - последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, D(X1)<C, D(X2)<C,… D(Хk)<C,… то, каково бы ни было постоянное ε > 0,
С точки зрения прикладной статистики ограниченность дисперсий вполне естественна. Она вытекает, например, из ограниченности диапазона изменения практически всех величин, используемых при реальных расчетах. В 1923 г. А.Я. Хинчин показал, что если случайные величины не только независимы, но и одинаково распределены, то существование у них математического ожидания является необходимым и достаточным условием для применимости закона больших чисел [2, с.150]. Теорема [2, с.150-151]. Для того чтобы для последовательности Х1, Х2,…, Хk ,…, (как угодно зависимых) случайных величин при любом положительном ε выполнялось соотношение (3), необходимо и достаточно, чтобы при n→ ∞
Законы больших чисел для случайных величин служат основой для аналогичных утверждений для случайных элементов в пространствах более сложной природы. В частности, в пространствах произвольной природы (см. главу 2). Однако здесь мы ограничимся классическими формулировками, служащими основой для современной прикладной статистики. Смысл классических законов больших чисел состоит в том, что выборочное среднее арифметическое независимых одинаково распределенных случайных величин приближается (сходится) к математическому ожиданию этих величин. Другими словами, выборочные средние сходятся к теоретическому среднему. Это утверждение справедливо и для других видов средних. Например, выборочная медиана сходится к теоретической медиане. Это утверждение – тоже закон больших чисел, но не классический. Существенным продвижением в теории вероятностей во второй половине ХХ в. явилось введение средних величин в пространствах произвольной природы и получение для них законов больших чисел, т.е. утверждений, состоящих в том, что эмпирические (т.е. выборочные )средние сходятся к теоретическим средним. Эти результаты рассмотрены в главе 2.
|
||
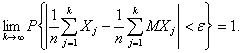 (3)
(3)