«Управление и Оптимизация Производственного Предприятия»
|
|
|
||||||||||||||||
|
М.: Издательство «Экзамен», 2004. 2.2.2. Одношаговые оценки Одношаговые оценки имеют столь же хорошие асимптотические свойства, что и оценки максимального правдоподобия, при тех же условиях регулярности, что и ОМП. Грубо говоря, они представляют собой результат первой итерации при решении системы уравнений максимального правдоподобия по методу Ньютона-Ватсона. Одношаговые оценки выписываются в виде явных формул, а потому требуют существенно меньше машинного времени, а также могут применяться при ручном счете (на калькуляторах). Снимаются вопросы о сходимости алгоритмов, о выборе момента прекращения вычислений, о влиянии округлений при вычислениях на окончательный результат. ОШ оценки были использованы нами при разработке ГОСТ 11.011-83 вместо ОМП. Как и раньше, рассмотрим выборку x1, x2,…, xn из распределения с плотностью f(x;θ0), где f(x;θ0)- элемент параметрического семейства плотностей распределения вероятностей {f(x;θ), θєΘ}. Здесь Θ – известное статистику k-мерное пространство параметров, являющееся подмножеством евклидова пространства Rk, а конкретное значение параметра θ0 неизвестно. Его и будем оценивать. Обозначим θ =(θ1, θ2,…, θk). Рассмотрим вектор-столбец частных производных логарифма плотности вероятности
и матрицу частных производных второго порядка для той же функции
Положим
Пусть матрица информации Фишера I(θ0) = M[-bn(θ0)] положительно определена. Определение 1 [10, с.269]. Оценку θ(n) параметра θ0 называют наилучшей асимптотически нормальной оценкой (сокращенно НАН-оценкой), если распределение случайного вектора Определение 1 корректно: I-1(θ0) является нижней асимптотической границей для ковариационной матрицы случайного вектора Для анализа реальных данных естественно рекомендовать какую-либо из НАН-оценок. (Это утверждение всегда верно на этапе асимптотики при изучении конкретной задачи прикладной статистики. Теоретически можно предположить, что при тщательном изучении для конкретных конечных объемов выборки наилучшей окажется какая-либо оценка, не являющаяся НАН-оценкой. Однако такие ситуации нам пока не известны.) Пусть θ1(n) и Определение 2. Одношаговой оценкой (ОШ-оценкой, или ОШО) называется оценка
Теорема 1 [14]. Пусть выполнены следующие условия. (I) Распределение (II) При некотором ε > 0 и n → ∞
(III) Для любого ε > 0
Тогда ОШ-оценка является НАН-оценкой. Доказательство. Рассмотрим тождество
В силу условия (II) теоремы
Из условия (I) теоремы следует, что первое слагаемое в правой части формулы (2) сходится при n → ∞ по распределению к нормальному закону с математическим ожиданием 0 и ковариационной матрицей I-1(θ0). Согласно условию (III)
по вероятности. Кроме того, согласно тому же условию последовательность матриц
по вероятности. Левая часть формулы (3) преобразуется к виду
где Е – единичная матрица. Поскольку из условия (I) теоремы следует, что для bn(θ0) справедлива (многомерная) центральная предельная теорема, то
С учетом условия (III) теоремы заключаем, что
Из соотношений (4), (5) и условия (III) теоремы вытекает справедливость формулы (3). Теорема доказана. Прокомментируем условия теоремы. Условия (I) и (II) обычно предполагаются справедливыми при рассмотрении оценок максимального правдоподобия [10]. Эти условия можно выразить в виде требований, наложенных непосредственно на плотность f(x;θ) из параметрического семейства, как это сделано, например, в [13]. Условие (III) теоремы, наложенное на исходные оценки, весьма слабое. Обычно используемые оценки θ1(n) и Какие оценки годятся в качестве начальных? В качестве θ1(n) можно использовать оценки метода моментов, как это сделано в ГОСТ 11.011-83 [1], или, например, квантильные. В качестве
Для гамма-распределения с неизвестными параметрами формы, масштаба и сдвига ОШ-оценки применены в [1]. При этом оценка (6) оказалась непрактичной, поскольку с точностью до погрешностей измерений и вычислений det(bn) = 0 для реальных данных о наработке резцов до предельного состояния, приведенных выше в табл.2 (пункт 2.2.1). Поскольку det(bn) = 0, то обратная матрица не существует, вычисления по формуле (6) невозможны. Поэтому в [1] в качестве ОШ-оценки была применена непосредственно первая итерация метода Ньютона-Рафсона решения системы уравнений максимального правдоподобия, т.е. была использована оценка
В формуле (7) непосредственно используется явный вид зависимости матрицы информации Фишера от неизвестных параметров распределения. В других случаях выбор тех или иных начальных оценок, в частности, выбор между (6) и (7), может определяться, например, простотой вычислений. Можно использовать также устойчивые аналоги [5] перечисленных выше оценок. Полезно отметить, что еще в 1925 г., т.е. непосредственно при разработке метода максимального правдоподобия, его создатель Р.Фишер считал, что первая итерация по методу Ньютона-Рафсона дает хорошую оценку вектору неизвестных параметров [10, с.298]. Он однако рассматривал эту оценку как аппроксимацию ОМП. А.А.Боровков воспринимает ОШ-оценки как способ «приближенного вычисления оценок максимального правдоподобия» [15, с.225] и показывает асимптотическую эквивалентность ОШ-оценок и ОМП (в более сильных предположениях, чем в теореме 1; другими словами, теорема 1 обобщает результаты А.А. Боровкова относительно ОШ-оценок). Мы же полагаем, что ОШ-оценки имеют самостоятельную ценность, причем не меньшую, а в ряде случаев большую, чем ОМП. По нашему мнению, ОМП целесообразно применять (на этапе асимптотики) только тогда, когда они находятся явно. Во всех остальных случаях следует использовать на этом этапе ОШ-оценки (или какие-либо иные, выбранные из дополнительных соображений). С чем связана популярность оценок максимального правдоподобия? Из всех НАН-оценок они наиболее просто вводятся, ранее других предложены. Поэтому среди математиков сложилась устойчивая традиция рассматривать ОМП в курсах математической статистики. Однако при этом игнорируются вычислительные вопросы, а также отодвигаются в сторону многочисленные иные НАН оценки. В прикладной статистике – иные приоритеты. На первом месте – ОШ-оценки, все остальные НАН-оценки, в том числе ОМП, рассматриваются в качестве дополнительных возможностей. Пример 1. Найдем ОШ-оценки для гамма-распределения с плотностью
Плотность вероятности в формуле (8) определяется тремя параметрами a, b, c, где a>0, b>0. При этом a является параметром формы, b - параметром масштаба и с - параметром сдвига. Здесь Γ(а) - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (8),
Как следует из явного вида плотности (8), логарифмическая функция правдоподобия имеет вид [16, с. 98]:
а уравнения правдоподобия таковы:
где
Ясно, что выписанная система нелинейных уравнений не имеет аналитического решения, в отличие от аналогичной системы для семейства нормальных распределений. Построим ОШ-оценки для задачи оценивания трех неизвестных параметров [17]. В качестве начальных оценок θ1(n) будем использовать оценки метода моментов (см. пункт 2.2.1):
где Матрица информации Фишера согласно [16, с.98] при a > 2 имеет вид
Вектор-столбец частных производных логарифма плотности вероятности
имеет координаты
Таким образом, для получения sn(a*, b*, c*) необходимо вычислить две суммы
и произвести еще несколько арифметических действий, число которых не зависит от объема выборки. Одношаговые оценки an, bn, cn для параметров гамма-распределения вычисляют по формуле
где I-1 – обратная матрица к матрице информации Фишера I, заданной формулой (9). Матрицу I-1 нетрудно рассчитать аналитически. Формулы для нахождения одношаговых оценок расписаны в [1]. Расчеты облегчает то обстоятельство, что для гамма-распределения вторая координата вектора sn(a*, b*, c*) тождественно равна 0, т.е. sn(2)(a*, b*, c*) ≡ 0. При n → ∞ распределение вектора оценок (an, bn, cn) приближается трехмерным нормальным распределением с математическим ожиданием, равным вектору истинных значений параметров (a, b, c), и ковариационной матрицей I-1(an, bn, cn). На этом приближении основаны правила расчета доверительных границ для параметров гамма-распределения [1]. Дисперсии оценок неизвестны, но зато имеются известные статистику зависимости этих дисперсий от параметров гамма-распределения. Эти зависимости непрерывные. Они стоят на главной диагонали ковариационной матрицы I-1(an,bn, cn). Поэтому можно вместо неизвестных параметров подставить в них оценки этих параметров и на основе принципа наследования сходимости (глава 1.4 выше) получить состоятельные оценки дисперсий. Затем на основе оценок дисперсий обычным образом строятся доверительные интервалы для параметров гамма-распределения. В табл.1 приведены результаты реализации описанной выше схемы расчетов - точечные и интервальные (при односторонней доверительной вероятности 0,95) оценки параметров гамма-распределения для данных, содержащихся в табл.2 предыдущего пункта 2.2.1. Таблица 1. Одношаговые оценки и доверительные границы для параметров гамма-распределения
Приведенные в табл.1 данные получены на основе асимптотических формул. Из-за конечности объема выборки необходимо внести некоторые коррективы. Поскольку параметр формы всегда положителен, a > 0, то нижняя доверительная граница для этого параметра должна быть неотрицательна, следует положить aH = 0. Поскольку плотность гамма-распределения положительна только правее параметра с, то, очевидно, c < xmin = 9,00, верхняя доверительная граница для параметра сдвига должна быть заменена на cB = 9,00. Может ли параметр сдвига быть отрицательным в данной прикладной задаче? Отрицательность параметра сдвига означает, что с положительной вероятностью рассматриваемая случайная величина отрицательна. Т.е. наработка резца до предельного состояния отрицательна. Ясно, что такого быть не может, хотя для специалиста по математической статистике отрицательность параметра сдвига вполне приемлема. Однако специалист по прикладной статистике должен признать неотрицательность параметра с при обработке данных, составляющих рассматриваемую выборку. Следовательно, нижнюю доверительную границу для параметра сдвига необходимо заменить на сн = 0. Как следует из проведенных выше рассуждений и выкладок (см. также [16, с.98-100]), отношение дисперсий оценок метода моментиов и ОШ-оценок имеет вид
при больших а. Это отношение, как и должно быть из общих соображений, всегда меньше 1. Отношение дисперсий возрастает при приближении к 0 коэффициента асимметрии распределения. Если a > 39,1 (коэффициент асимметрии меньше 0,102), то эффективность оценки метода моментов превышает 80%. При а = 20 (коэффициент асимметрии 0,20) она равна 65%. Напомним, что при безграничном росте параметра формы а гамма-распределение приближается к нормальному, для которого оценки метода моментов и ОМП совпадают, а потому имеют равные дисперсии. Поэтому вполне естественно, что отношение дисперсий в формуле (10) стремится к 1 при безграничном росте параметра формыа. Хотя дисперсии оценок метода моментов, как правило, меньше, чем дисперсии НАН-оценок, таких, как ОШО и ОМП, метод моментов играет большую роль в прикладной статистике. Во-первых, обычно их расчет проще (в частности, требует меньшего числа компьютерных операций), чем оценок других типов. К тому же оценки находятся с помощью выборочных моментов, которые, как правило, вычисляются на этапе описания статистических данных. Во-вторых, они служат основой для вычисления оценок других типов, например, ОШО. Для запуска итерационных методов нахождения ОМП также нужны начальные значения, и ими обычно являются оценки метода моментов. В-третьих, при учете погрешностей результатов наблюдений оценки метода моментов могут оказаться точнее ОМП и асимптотически эквивалентных им ОШО (см. главу 3.5 настоящего учебника). Методы оценивания параметров гамма-распределения и примеры расчетов для всех семи постановок, перечисленных в табл.1 пункта 2.2.1, приведены в [1]. Большинство из них основано на асимптотических (при n → ∞) теоретических результатах прикладной статистики. Методом статистических испытаний (Монте-Карло) показано, что уже при n > 10 используемые приближения удовлетворительны. Другими словами, асимптотической нормальностью оценок и другими важными для проведенных выше рассуждений предельными результатами можно пользоваться уже при n > 10. Алгоритмическое и программное обеспечение ОШ-оценок для распределения Вейбулла-Гнеденко и гамма-распределения рассмотрено в содержательной монографии [18]. История вопроса освещена в статье [14].
|
|||||||||||||||||
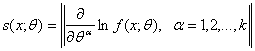
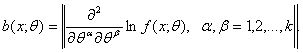
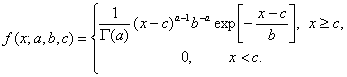 (8)
(8)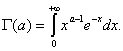
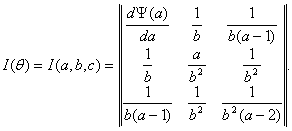 (9)
(9)