«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
М.: Издательство «Экзамен», 2004. 3.2.5. Статистические методы классификации Рассмотрим с позиций прикладной статистики несколько конкретных вопросов теории классификации. Вероятностная теория кластер-анализа. Как и для прочих статистических методов, свойства алгоритмов кластер-анализа необходимо изучать на вероятностных моделях. Это касается, например, условий естественного объединения двух кластеров. Вероятностные постановки нужно применять, в частности, при перенесении результатов, полученных по выборке, на генеральную совокупность. Вероятностная теория кластер-анализа и методов группировки различна для исходных данных типа таблиц «объект × признак» и матриц сходства. Для первых параметрическая вероятностно-статистическая теория называется "расщеплением смесей". Непараметрическая теория основана на непараметрических оценках плотностей вероятностей и их мод. Основные результаты, связанные с непараметрическими оценками плотности, обсуждались в главе 2.1. Если исходные данные - матрица сходства ||d(x,y)||, то необходимо признать, что развитой вероятностно-статистической теории пока нет. Подходы к ее построению намечены в работе [9]. Одна из основных проблем - проверка "реальности" кластера, его объективного существования независимо от расчетов исследователя. Проблема "реальности" кластера давно обсуждается специалистами различных областей. Типичное рассуждение таково. Предположим, что результаты наблюдений можно рассматривать как выборку из некоторого распределения с монотонно убывающей плотностью при увеличении расстояния от некоторого центра. Примененный к подобным данным какой-либо алгоритм кластер-анализа порождает некоторое разбиение. Ясно, что оно - чисто формальное, поскольку выделенным таксонам (кластерам) не соответствуют никакие "реальные" классы. Другими словами, задача кластер-анализа не имеет решения, а алгоритм дает лишь группировку. При обработке реальных данных мы не знаем вида плотности. Проблема состоит в том, чтобы определить, каков результат работы алгоритма (реальные кластеры или формальные группы). Частный случай этой проблемы - проверка обоснованности объединения двух кластеров, которые мы рассматриваем как два множества объектов, а именно, множества {a1, a2,…, ak} и {b1, b2,…, bm}. Пусть, например, используется алгоритм типа "Дендрограмма". Естественной представляется следующая идея. Пусть есть две совокупности мер близости. Одна - меры близости между объектами, лежащими внутри одного кластера, т.е. d(ai,aj),1<i<j<k, d(ba,bb), 1<a<b<m. Другая совокупность - меры близости между объектами, лежащими в разных кластерах, т.е. d(ai,ba), 1<i<k, 1<a<m. Эти две совокупности мер близости предлагается рассматривать как независимые выборки и проверять гипотезу о совпадении их функций распределения. Если гипотеза не отвергается, объединение кластеров считается обоснованным; в противном случае - объединять нельзя, алгоритм прекращает работу. В рассматриваемом подходе есть две некорректности (см. также работу [9, разд.4]). Во-первых, меры близости не являются независимыми случайными величинами. Во-вторых, не учитывается, что объединяются не заранее фиксированные кластеры (с детерминированным составом), а полученные в результате работы некоторого алгоритма, и их состав (в частности, количество элементов) оказывается случайным. От первой из этих некорректностей можно частично избавиться. Справедливо следующее утверждение. Теорема 1. Пусть a1, a2,…, ak, b1, b2,…, bm - независимые одинаково распределенные случайные величины (со значениями в произвольном пространстве). Пусть случайная величина d(а1,а2) имеет все моменты. Тогда при k,т®¥ распределение статистики
(где U - сумма рангов элементов первой выборки в объединенной выборке; первая выборка составлена из внутрикластерных расстояний (мер близости) d(ai,aj), 1<i<j<k, и d(ba,bb), 1<a<b<m, а вторая - из межкластерных расстояний d(ai,ba), 1<i<k, 1<a<m) сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. На основе теоремы 1 очевидным образом формулируется правило проверки обоснованности объединения двух кластеров. Другими словами, мы проверяем статистическую гипотезу, согласно которой объединение двух кластеров образует однородную совокупность. Если величина U слишком мала, статистическая гипотеза однородности отклоняется (на заданном уровне значимости), и возможность объединения отбрасывается. Таким образом, хотя расстояния между объектами в кластерах зависимы, но эта зависимость слаба, и доказана математическая теорема о допустимости применения критерия Вилкоксона для проверки возможности объединения кластеров. О вычислительной сходимости алгоритмов кластер-анализа. Алгоритмы кластер-анализа и группировки зачастую являются итерационными. Например, формулируется правило улучшения решения задачи кластер-анализа шаг за шагом, но момент остановки вычислений не обсуждается. Примером является известный алгоритм "Форель", в котором постепенно улучшается положение центра кластера. В этом алгоритме на каждом шаге строится шар определенного заранее радиуса, выделяются элементы кластеризуемой совокупности, попадающие в этот шар, и новый центр кластера строится как центр тяжести выделенных элементов. При анализе алгоритма «Форель» возникает проблема: завершится ли процесс улучшения положения центра кластера через конечное число шагов или же он может быть бесконечным. Она получила название «проблема остановки». Для широкого класса так называемых "эталонных алгоритмов" проблема остановки была решена в работе [9]: процесс улучшения остановится через конечное число шагов. Отметим, что алгоритмы кластер-анализа могут быть модифицированы разнообразными способами. Например, описывая алгоритм "Форель" в стиле статистики объектов нечисловой природы, заметим, что вычисление центра тяжести для совокупности многомерных точек – это нахождение эмпирического среднего для меры близости, равной квадрату евклидова расстояния. Если взять более естественную меру близости – само евклидово расстояние, то получим алгоритм кластер-анализа "Медиана", отличающийся от "Форели" тем, что новый центр строится не с помощью средних арифметических координат элементов, попавших в кластер, а с помощью медиан. Проблема остановки возникает не только при построении диагностических классов. Она принципиально важна, в частности, и при оценивании параметров вероятностных распределений методом максимального правдоподобия. Обычно не представляет большого труда выписать систему уравнений максимального правдоподобия и предложить решать ее каким-либо численным методом. Однако когда остановиться, сколько итераций сделать, какая точность оценивания будет при этом достигнута? Общий ответ, видимо, невозможно найти, но обычно нет ответа и для конкретных семейств распределения вероятностей. Именно поэтому нет оснований рекомендовать решать системы уравнений максимального правдоподобия. Вместо них целесообразно использовать т.н. одношаговые оценки (подробнее см. об этих оценках главу 2.2). Эти оценки задаются конечными формулами, но асимптотически столь же хороши (на профессиональном языке - эффективны), как и оценки максимального правдоподобия. О сравнении алгоритмов диагностики по результатам обработки реальных данных. Перейдем к этапу применения диагностических правил, когда классы, к одному из которых нужно отнести вновь поступающий объект, уже выделены. В прикладных исследованиях применяют различные методы дискриминантного анализа, основанные на вероятностно-статистических моделях, а также с ними не связанные, т.е. эвристические, использующие детерминированные методы анализа данных. Независимо от "происхождения", каждый подобный алгоритм должен быть исследован как на параметрических и непараметрических вероятностно-статистических моделях порождения данных, так и на различных массивах реальных данных. Цель исследования - выбор наилучшего алгоритма в определенной области применения, включение его в стандартные программные продукты, методические материалы, учебные программы и пособия. Но для этого надо уметь сравнивать алгоритмы по качеству. Как это делать? Часто используют такой показатель качества алгоритма диагностики, как "вероятность правильной классификации" (при обработке конкретных данных - "частота правильной классификации"). Чуть ниже мы покажем, что этот показатель качества некорректен, а потому пользоваться им не рекомендуется. Целесообразно применять другой показатель качества алгоритма диагностики - оценку специального вида т.н. "расстояния Махаланобиса" между классами. Изложение проведем на примере разработки программного продукта для специалистов по диагностике материалов. Прообразом является диалоговая система «АРМ материаловеда», разработанная Институтом высоких статистических технологий и эконометрики для ВНИИ эластомерных материалов. При построении информационно-исследовательской системы диагностики материалов (ИИСДМ) возникает задача сравнения прогностических правил «по силе». Прогностическое правило - это алгоритм, позволяющий по характеристикам материала прогнозировать его свойства. Если прогноз дихотомичен («есть» или «нет»), то правило является алгоритмом диагностики, при котором материал относится к одному из двух классов. Ясно, что случай нескольких классов может быть сведен к конечной последовательности выбора между двумя классами. Прогностические правила могут быть извлечены из научно-технической литературы и практики. Каждое из них обычно формулируется в терминах небольшого числа признаков, но наборы признаков сильно меняются от правила к правилу. Поскольку в ИИСДМ должно фиксироваться лишь ограниченное число признаков, то возникает проблема их отбора. Естественно отбирать лишь те их них, которые входят в наборы, дающие наиболее «надежные» прогнозы. Для придания точного смысла термину «надежный» необходимо иметь способ сравнения алгоритмов диагностики по прогностической "силе". Результаты обработки реальных данных с помощью некоторого алгоритма диагностики в рассматриваемом случае двух классов описываются долями: правильной диагностики в первом классе При изучении качества алгоритмов классификации их сравнивают по результатам дискриминации вновь поступающей контрольной выборки. Именно по контрольной выборке определяются величины Нередко как показатель качества алгоритма диагностики (прогностической «силы») используют долю правильной диагностики
Однако показатель Другими словами, по доле правильной классификации алгоритм академика И.М. Гельфанда оказался хуже тривиального - объявить всех больных легкими, не требующими специального наблюдения. Этот вывод очевидно нелеп. И причина появления нелепости вполне понятна. Хотя доля тяжелых больных невелика, но смертельные исходы сосредоточены именно в этой группе больных. Поэтому целесообразна гипердиагностика - рациональнее часть легких больных объявить тяжелыми, чем сделать ошибку в противоположную сторону. Применение теории статистических решений в рассматриваемой постановке вряд ли возможно, поскольку оценить количественно потери от смерти больного нельзя по этическим соображениям. Поэтому, на наш взгляд, долю правильной диагностики Применение теории статистических решений требует знания потерь от ошибочной диагностики, а в большинстве научно-технических и экономических задач определить потери, как уже отмечалось, сложно. В частности, из-за необходимости оценивать человеческую жизнь в денежных единицах. По этическим соображениям это, на наш взгляд, недопустимо. Сказанное не означает отрицания пользы страхования, но, очевидно, страховые выплаты следует рассматривать лишь как способ первоначального смягчения потерь от утраты близких. Для выявления информативного набора признаков целесообразно использовать метод пересчета на модель линейного дискриминантного анализа, согласно которому статистической оценкой прогностической "силы" является
где Пример 1. Если доли правильной классификации κ = 0,90 и λ = 0,80, то Φ-1(κ) = 1,28 и Φ-1(λ) = 0,84, откуда d*= 2,12 и прогностическая сила δ* = Φ-1(1,06) = 0,86. При этом доля правильной классификации μ может принимать любые значения между 0,80 и 0,90, в зависимости от доли элементов того или иного класса среди анализируемых данных. Если классы описываются выборками из многомерных нормальных совокупностей с одинаковыми матрицами ковариаций, а для классификации применяется классический линейный дискриминантный анализ Р.Фишера, то величина Пусть алгоритм классификации применялся к совокупности, состоящей из т объектов первого класса и nобъектов второго класса. Теорема 2. Пусть т, п®¥. Тогда для всех х
где
С помощью теоремы 2 по Пример 2. В условиях примера 1 при m = n = 100 найдем асимптотическое среднее квадратическое отклонениеА(0,90; 0,80). Поскольку φ(Φ-1(κ)) = φ(1,28) = 0,176, φ(Φ-1(λ)) = φ(0,84) = 0,280, φ(d*/2) = φ(1,06) = 0,227, то подставляя в выражение для А2 численные значения, получаем, что
(численные значения плотности стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1 и функции, обратной к функции этого распределения, можно было взять, например, из справочника [4]). При m = n = 100 имеем А(0,90; 0,80) = 0,0252. При доверительной вероятности γ = 0,95 имеем u(0,95) = Φ-1(1,0,975) = 1,96, а потому нижняя доверительная граница для прогностической силы δ есть δН = 0,86 – 1,96 × 0,0252 = 0,81, а верхняя доверительная граница такова: δВ = 0,86 + 1,96 × 0,0252 = 0,91. Аналогичный расчет при m =n = 1000 дает δН = 0,845, δВ = 0,875. Как проверить обоснованность пересчета на модель линейного дискриминантного анализа? Допустим, что классификация состоит в вычислении некоторого прогностического индекса у и сравнении его с заданным порогом с. Объект относят к первому классу, если у<с, ко второму, если у>с. Прогностический индекс – это обычно линейная функция от характеристик рассматриваемых объектов. Другими словами, от координат векторов, описывающих объекты. Возьмем два значения порога с1 и c2. Если пересчет на модель линейного дискриминантного анализа обоснован, то , как можно показать, "прогностические силы" для обоих правил совпадают: Пусть
Теорема 3. Если истинные прогностические силы двух правил диагностики совпадают,
где
Из теоремы 3 вытекает метод проверки рассматриваемой гипотезы: при выполнении неравенства
она принимается на уровне значимости, асимптотически равном Пример 3. Пусть данные примеров 1 и 2 соответствуют порогу с1. Пусть порогу с2 соответствуют κ’ = 0,95 и λ’ = 0,70. Тогда в обозначениях теоремы 3 κ1 = 0,90, κ2 = 0,05, λ2 = 0,10, λ3 = 0,70. Далее d*(c1) = 2,12 (пример 1), d*(c2) = 2,17, T(κ1, κ2) = 2,22, T(λ3, λ2) = 0,89. Гипотеза о совпадении прогностических сил на двух порогах принимается на уровне значимости α = 0,05 тогда и только тогда, когда
т.е. когда
Так, гипотеза принимается при m = n = 1000 и отвергается при m = n = 5000. Подходы к построению прогностических правил. Для решения задач диагностики используют два подхода – параметрический и непараметрический. Первый из них обычно основан на использовании того или иного индекса и сравнения его с порогом. Индекс может быть построен по статистическим данным, например, как в уже упомянутом линейном дискриминантном анализе Фишера. Часто индекс представляет собой линейную функцию от характеристик, выбранных специалистами предметной области, коэффициенты которой подбирают эмпирически. Непараметрический подход связан с леммой Неймана-Пирсона в математической статистике и с теорией статистических решений. Он опирается на использование непараметрических оценок плотностей распределений вероятностей, описывающих диагностические классы. Обсудим ситуацию подробнее. Математические методы диагностики, как и статистические методы в целом, делятся на параметрические и непараметрические. Первые основаны на предположении, что классы описываются распределениями из некоторых параметрических семейств. Обычно рассматривают многомерные нормальные распределения, при этом зачастую принимают гипотезу о том, что ковариационные матрицы для различных классов совпадают. Именно в таких предположениях сформулирован классический дискриминантный анализ Фишера. Как известно, обычно нет оснований считать, что наблюдения извлечены из нормального распределения. Поэтому более корректными, чем параметрические, являются непараметрические методы диагностики. Исходная идея таких методов основана на лемме Неймана-Пирсона, входящей в стандартный курс математической статистики. Согласно этой лемме решение об отнесении вновь поступающего объекта (сигнала, наблюдения и др.) к одному из двух классов принимается на основе отношения плотностей f(x)/g(x), где f(x) - плотность распределения, соответствующая первому классу, а g(x) - плотность распределения, соответствующая второму классу. Если плотности распределения неизвестны, то применяют их непараметрические оценки, построенные по обучающим выборкам. Пусть обучающая выборка объектов из первого класса состоит из n элементов, а обучающая выборка для второго класса - из m объектов. Тогда рассчитывают значения непараметрических оценок плотностей fn(x) и gm(x) для первого и второго классов соответственно, а диагностическое решение принимают по их отношению. Таким образом, для решения задачи диагностики достаточно научиться строить непараметрические оценки плотности для выборок объектов произвольной природы. Методы построения непараметрических оценок плотности распределения вероятностей в пространствах произвольной природы рассмотрены в главе 2.1.
|
||
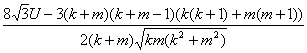
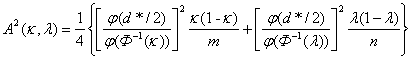 ;
;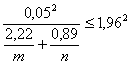 ,
,