«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
М.: Издательство «Экзамен», 2004. 1.1.6. Аксиоматическое введение расстояний В прикладной статистике используют большое количество метрик и показателей различия (см. примеры в предыдущем пункте). Как обоснованно выбрать то или иное расстояние для использования в конкретной задаче? В1959 г. американский статистик Джон Кемени предложил использовать аксиоматический подход, согласно которому следует сформулировать естественные для конкретной задачи аксиомы и вывести из них вид метрики. Этот подход получил большую популярность в нашей стране после выхода в 1972 г. перевода на русский язык книги Дж. Кемени и Дж. Снелла [19], в которой дана система аксиом для расстояния Кемени между упорядочениями. (Упорядочения, как и иные бинарные отношения, естественно представить в виде квадратных матриц из 0 и 1; тогда расстояние Кемени – это расстояние из примера 7 предыдущего пункта.) Последовала большая серия работ, в которых из тех или иных систем аксиом выводился вил метрики или показателя различия для различных видов данных, прежде всего для объектов нечисловой природы. Многие полученные результаты описаны в обзоре [20], содержащем 161 ссылку, в том числе 69 на русском языке. Рассмотрим некоторые из них. Аксиоматическое введение расстояния между толерантностями. Толерантность - это бинарное отношение, являющееся рефлексивным и симметричным. Его обычно используют для описания отношения сходства между реальными объектами, отношений знакомства или дружбы между людьми. От отношения эквивалентности отличается тем, что свойство транзитивности не предполагается обязательно выполненным. Действительно, Иванов может быть знаком с Петровым, Петров – с Сидоровым, но при этом ничего необычного нет в том, что Иванов и Сидоров не знакомы между собой. Пусть множество Х, на котором определено отношение толерантности, состоит из конечного числа элементов: X= {x1, x2,…, xk}. Тогда толерантность описывается квадратной матрицей A = ||a(i,j)||, i,j = 1, 2,…, k, такой, что a(i,j) = 1, если xi и xj связаны отношением толерантности, и a(i,j) = 0 в противном случае. Матрица A симметрична: a(i,j) =a(j,i), на главной диагонали стоят единицы: a(i,i) = 1. Любая матрица, удовлетворяющая приведенным в предыдущей фразе условиям, является матрицей, соответствующей некоторому отношению толерантности. Матрице А можно сопоставить неориентированный граф с вершинами в точках Х: вершины xi и xj соединены ребром тогда и только тогда, когда a(i,j) = 1. Толерантности используются, в частности, при проведении экспертных исследований (см. пункт 3.4.7 ниже). Будем говорить, что толерантность А3 лежит между толерантностями А1 и А2, если при всех i, j число a3(i,j) лежит между числами a1(i,j) и a2(i,j), т.е. выполнены либо неравенства a1(i,j) <a3(i,j) < a2(i,j), либо неравенства a1(i,j)> a3(i,j) > a2(i,j). Теорема 1 [2]. Пусть (I) d(A1, A2) – метрика в пространстве толерантностей, определенных на конечном множестве X = {x1, x2,…, xk}; (II) d(A1, A3) + d(A3, A2) = d(A1, A2) тогда и только тогда, когда A3 лежит между A1 и A2; (III) если отношения толерантности A1 и A2 отличаются только на одной паре элементов, т.е. a1(i,j) = a2(i,j) при (i,j) ≠ (i0,j0), i<j, i0 < j0, и a1(i0, j0) ≠ a2(i0, j0), то d(A1, A2) = 1. Тогда
Таким образом, расстояние d(A1, A2) только постоянным множителем ½ отличается от расстояния Кемени, введенного в пространстве всех бинарных отношений как расстояние Хемминга между описывающими отношения матрицами из 0 и 1 (см. пример 7 предыдущего пункта). Теорема 1 дает аксиоматическое введение расстояния в пространстве толерантностей. Оказалось, что оно является сужением расстояния Кемени на это пространство. Сам Дж. Кемени дал аналогичную систему аксиом для сужения на пространство упорядочений. Доказательство теоремы 1 вытекает из рассмотрений, связанных с аксиоматическим введением расстояний между множествами, и приводится ниже. Мера симметрической разности как расстояние между множествами. Как известно, бинарное отношение можно рассматривать как подмножество декартова квадрата Х2 того множества Х, на котором оно определено. Поэтому теорему 1 можно рассматривать как аксиоматическое введение расстояния между множествами специального вида. Укажем систему аксиом для расстояния между множествами общего вида, описанного в примере 9 предыдущего пункта. Определение 1. Множество В находится между множествами А и С, если С помощью определения 1 в совокупности множеств вводятся геометрические соотношения, использование которых полезно для восприятия рассматриваемых ситуаций. Расстояние между двумя точками в евклидовом пространстве не изменится, если обе точки сдвинуть на один и тот же вектор. Аналогичное свойство расстояния между множествами сформулируем в виде аксиомы 1. Оно соответствует аксиоме 3 Кемени и Снелла [19, с.22] для расстояний между упорядочениями. Аксиома 1. Если Определение 2. Непустая система множеств называется кольцом, если для любых двух входящих в нее множеств в эту систему входят их объединение, пересечение и разность. Множество Х называется единицей системы множеств, если оно входит в эту систему, а все остальные множества системы являются подмножествами Х. Кольцо множеств, содержащее единицу, называется алгеброй множеств [21, с.38]. Теорема 2. Пусть W - алгебра множеств, d: W2 → R1. Тогда аксиома 1 эквивалентна следующему условию:d(A,B) = d(A\B, B\A) для любых A, B є W. Доказательство. Поскольку
то равенство d(A,B) = d(A\B, B\A) следует из аксиомы 1. Обратное утверждение вытекает из того, что в условиях аксиомы 1
Теорема 2 доказана. С целью внести в алгебру множеств W отношение «находиться между», аналогичное используемому при аксиоматическом введении расстояний в пространствах бинарных отношений (см. условие (II) в теореме 1), примем следующую аксиому. Аксиома 2. Если В лежит между А и С, то d(A,B)+d(B,C)= d(A,C). Определение 3. Неотрицательная функция μ, определенная на алгебре множеств W, называется мерой, если для любых двух непересекающихся множеств А и В из W справедливо соотношение
Теорема 3. Пусть W – алгебра множеств, аксиомы 1 и 2 выполнены для функции d: W2 → [0;+∞]. Функция dсимметрична: d(A,B) = d(B,A) для любых А и В из W. Тогда существует, и притом единственная, мера μ на W такая, что
при всех А и В из W, где АΔВ – симметрическая разность множеств А и В, т.е. Доказательство. Положим
Покажем, что определенная формулой (2) функция множества μ является мерой. Неотрицательность μ следует из неотрицательности d. Остается доказать аддитивность, т.е. что из
Поскольку А всегда лежит между
Если А∩В= Докажем соотношение (1). Поскольку А\B и B\A имеют пустое пересечение, то согласно определению 1 пустое множество
Из симметричности и соотношения (2) следует, что
откуда d(A\B, B\A)= μ(A\B) + μ(B\A). Из соотношения (3) следует, что μ(A\B) + μ(B\A) = μ(AΔB). С другой стороны, по аксиоме 1
Из трех последних равенств вытекает справедливость равенства (1). Остается доказать единственность меры μ в соотношении (1). Поскольку АΔВ = В при А = Теорема 4 (обратная). Пусть μ – мера определенная на алгебре множеств W. Тогда функция d(A,B) = μ(AΔB) является псевдометрикой, для нее выполнены аксиомы 1 и 2. Доказательство. То, что функция d(A,B) из (1) задает псевдометрику, хорошо известно (см., например, [22, с.79]). Доказательство аксиомы 2 содержится в [23, c.181-183]. Аксиома 1 следует из того, что условия
Замечание. Полагая в аксиоме 2 А = В = С, получаем, что d(A,А) + d(A,А) = d(A,А), т.е. d(A,А) = 0. Согласно теоремам 3 и 4, из условий теоремы 3 следует неравенство треугольника. Таким образом, в теореме 3 действительно приведена система аксиом, определяющая семейство псевдометрик в пространстве множеств. Обсудим независимость (друг от друга) условий теоремы 3. Отбрасывание неотрицательности функции dприводит к тому, что слово «мера» в теоремах 3 и 4 необходимо заменить на «заряд» [21, с.328]. Этот термин обозначает аддитивную функцию множеств, не обладающую свойством неотрицательности. Заряд можно представить как разность двух мер. Функция Приведем пример системы множеств W и метрики в ней, для которых верна аксиома 2, но не верна аксиома 1, а потому эту метрику нельзя представить в виде (1). Пусть W состоит из множеств
Если единица Х алгебры множеств W конечна, т.е. X = {x1, x2,…, xk}, то расстояние (1) принимает вид
где χС – индикатор (индикаторная функция) множества С, т.е. χС(х) = 1, если х є С, и χС(х) = 0 в противном случае. Как следует из теоремы 3, неотрицательный коэффициент μi – это мера одноэлементного множества {xi}, а также расстояние этого множества от пустого множества, т.е.
Если все коэффициенты μi положительны, то формула (5) определяет метрику, если хотя бы один равен 0, то – псевдометрику, поскольку в таком случае найдутся два различающиеся между собой множества А и В такие, чтоd(A,B) = 0. Расстояние определяется однозначно, если априори известны коэффициенты μi. В частности, равноправность объектов (элементов единицы алгебры множеств Х) приводит к μi ≡ 1. Требование равноправности содержится в аксиомах 2 и 4 Кемени [19, с.21-22]. Применим полученные результаты к толерантностям и докажем теорему 1. Совокупность всех толерантностей, определенных на конечном множестве У, естественным образом ассоциируется с совокупностью всех подмножеств множества Х = {(yi, yj), 1 < i < j < k}. Именно, пара (yi, yj) входит в подмножество тогда и только тогда, когда yi и yjсвязаны отношением толерантности. Указанная совокупность подмножеств является алгеброй множеств с единицей Х. Определение 1 понятия «находиться между» для множеств полностью соответствует ранее данному определению понятия «находиться между» для толерантностей. Теорема 5. Пусть выполнены условия (I) и (II) теоремы 1 и аксиома 1. Тогда существуют числа μij > 0 такие, что
Для доказательства достаточно сослаться на теорему 3. Поскольку в условии (I) требуется, чтобы функцияd(A,B) являлась метрикой, то необходимо μij > 0. Теорема 6. Пусть выполнены условия теоремы 1 и, кроме того, аксиома 1. Тогда верно заключение теоремы 1. Доказательство. Рассмотрим толерантность А, для которой a(i,j) = 1 при (i,j) = (i0,j0) и a(i,j) = 0 в противном случае. Согласно условию (III) теоремы 1 Для окончательного доказательства теоремы 1 осталось избавиться от требования справедливости аксиомы 1. Доказательство теоремы 1. Рассмотрим две толерантности А и В такие, что при представлении их в виде множеств
По условию (III) Поскольку А∩В лежит между А и В, то по условию (II) d(A, B) = d(А∩В, A) + d(А∩В, B). При этом А∩В Замечание 1. Таким образом, условие (III) не только дает нормировку, но и заменяет аксиому 1. Замечание 2. Условие (I) теоремы 1 не использовалось в доказательстве, но было приведено в первоначальной публикации [24], чтобы подчеркнуть цель рассуждения. По той же причине оно сохранено в формулировке теоремы 1, хотя в доказательстве удалось без него обойтись. Понадобилась только симметричность функции d. Аксиоматическое введение метрики в пространстве неотрицательных суммируемых функций.Рассмотрим пространство L(E, μ) неотрицательных суммируемых функций на множестве E с мерой μ. Далее в настоящем пункте будем рассматривать только функции из L(E, μ). Интегрирование всюду проводится по пространствуЕ и по мере μ. Будем писать g = h или g < h, если указанные соотношения справедливы почти всюду по μ на Е (т.е. могут нарушаться лишь на множестве нулевой меры). Аксиоматически введем расстояние в пространстве L(E, μ) (изложение следует работе [25]). Обозначим M (g,h) = max (g , h) и m(g, h) = min (g, h). Пусть D: L(E, μ) × L(E, μ) → R1 – тот основной объект изучения, аксиомы для которого будут сейчас сформулированы. Аксиома 1. Если gh = 0, g + h ≠ 0, то D(g, h) = 1. Аксиома 2. Если h < g, то D(g, h) = C ∫ (g – h) dμ, где множитель С не зависит от h, т.е. C = C(g). Лемма. Из аксиом 1,2 следует, что для h < g ≠ 0
Для доказательства заметим, что по аксиоме 1 D(g, 0) =1, а по аксиоме 2 D(g, 0) = С ∫ g dμ, откуда С = (∫ gdμ)-1. Подставляя это соотношение в аксиому 2, получаем заключение леммы. Требование согласованности расстояния в пространстве L(E, μ) с отношением «находиться между» приводит, как и ранее для расстояния d(A, B), к следующей аксиоме. Аксиома 3. Для любых g и h справедливо равенство D(g, h) = D(M(g, h), g) + D(M(g, h), h). Замечание. В ряде реальных ситуаций естественно считать, что наибольшее расстояние между элементами пространства множеств (которое без ограничения общности можно положить равным 1), т.е. наибольшее несходство, соответствует множествам, не имеющим общих элементов. Расстояние, введенное в теореме 3 (формула (1)), этому условию не удовлетворяет. Поэтому в пространстве множеств была аксиоматически введена [20] так называемая D-метрика (от dissimilarity (англ.) – несходство), для которого это условие выполнено. Она имеет вид:
Приведенные выше аксиомы являются обобщениями соответствующих аксиом для D-метрики в пространстве множеств. Теорема 7. Из аксиом 1-3 следует, что
Доказательство. Поскольку (M(g, h) - g) + (M(g, h) – h) = |g – h|, то заключение теоремы 7 при g + h ≠ 0 вытекает из леммы и аксиомы 3. Из аксиомы 2 при g = 0 следует, что D(0, 0) = 0. Легко видеть, что функция D, заданная формулой (8), удовлетворяет аксиомам 1-3 и, кроме того, D(g, h) < 1 при любых g и h. Замечание. Если g и h – индикаторные функции множеств, то формула (8) переходит в формулу (7). Если g и h– функции принадлежности нечетких множеств, то формула (8) задает метрику в пространстве нечетких множеств, а именно, D-метрику в этом пространстве [20]. Теорема 8. Функция D(g,h), определенная формулой (8), является метрикой в L(E, μ) (при отождествлении функций, отличающихся лишь на множестве нулевой меры), причем D(g, f) + D(f, h) = D(g, h) тогда и только тогда, когда f = g, f = h или f = M(g, h). Доказательство. Обратимся к определению метрики. Для рассматриваемой функции непосредственно очевидна справедливость условий неотрицательности и симметричности. Очевидна и эквивалентность условия D(g, h) = 0 равенству g = h. Остается доказать неравенство треугольника и установить, когда оно обращается в равенство. Без ограничения общности можно считать, что рассматриваемые расстояния задаются верхней строкой формулы (8) и, кроме того, R = ∫ M(g, f) dμ - ∫ M(f, h) dμ > 0 (частные случаи с использованием нижней строки формулы (8) рассматриваются элементарно, а справедливости последнего неравенства можно добиться заменой обозначений функций – элементов пространства L(E, μ)). Тогда
причем равенство имеет место тогда и только тогда, когда R = 0 или f = h. Положим P = ∫ (|g – f| + |f – h| - |g – h|) dμ, Q = ∫ (M(g, f) – M(g, h)) dμ. Ясно, что P > 0 и
Если Q < 0, то, очевидно, неравенство треугольника выполнено, причем неравенство является строгим. Рассмотрим случай Q > 0. Воспользуемся следующим элементарным фактом: если y > x, y > 0, P >Q > 0, то
Из соотношений (10) и (11) вытекает, что для доказательства неравенства треугольника достаточно показать, что P – Q> 0. Рассмотрим k = {|g – f| + |f – h| - |g – h|} – M(g, f) + M(g, h). Применяя равенство (M(g, h) - g) + (M(g, h) – h) = |g – h| к слагаемым, заключенным в фигурные скобки, получаем, что k = M(f, h) + [M(g, f) + M(f, h) – M(g, h) – 2f]. Применяя соотношение M(g, h) = g + h – m(g, h) (12) К слагаемым, заключенным в квадратные скобки, получаем, что k = M(f, h) – m(f, h) – m(g, f) + m(g, h). Так как M(f, h) – m(f, h) = |f – h|, то k = |f – h| - (m(g, f) – m(g, h)) > (f – h) - (m(g, f) – m(g, h)). (13) В соответствии с (12) правая часть (13) есть M(g, f) – M(g, h), а потому P – Q = ∫ k dμ > Q > 0, что завершает доказательство для случая Q > 0. При этом неравенство треугольника является строгим. Осталось рассмотреть случай Q = 0. В силу соотношений (9) и (10) неравенство треугольника выполнено. Когда оно обращается в равенство? Тривиальные случаи: f = g или f = h. Если же f отлично от g и h, то необходимо, чтобы R= 0 и P = 0. Как легко проверить, последнее условие эквивалентно неравенствам m(g, h) < f < M(g, h). (14) Из правого неравенства в (14) следует, что M(g, f) < M(g, M(g, h)) = M(g, h). Так как Q = 0, то M(g, f) = M(g, h). Аналогичным образом из соотношений M(h, f) < M(h, M(g, h)) = M(g, h) = M(g, f) и R = 0 следует, что M(f, h) = M(g, h). Рассмотрим измеримое множество X = {x є E: h(x) < g(x)}. Тогда M(g, h) (x) = M(f, h) (x) = g(x) > h(x), т.е. h(x) < f(x) = M(g, h) (x) для почти всех x є X. Для почти всех y є {x є E: h(x) > g(x)} точно так же получаем f(y) = M(g, h) (y). Для почти всех z є {x є E: h(x) = g(x)} в силу (14) f(z) = M(g, h) (z), что и завершает доказательство теоремы. Замечание. Назовем функции g и h подобными, если существует число b > 0 такое, что g = bh. Тогда при 0 < b< 1 имеем D(g, h) = 1 – b, т.е. расстояние между подобными функциями линейно зависит от коэффициента подобия. Далее, пусть a > 0, тогда D(ag, ah) = D(g, h). Таким образом, метрика (8) инвариантна по отношению к преобразованиям подобия, которые образуют группу допустимых преобразований в шкале отношений. Это дает основания именовать метрику (8) метрикой подобия [25].
|
||
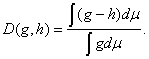
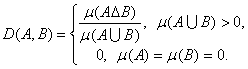 (7)
(7)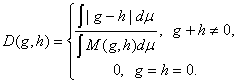 (8)
(8)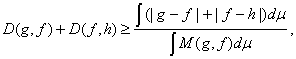 (9)
(9)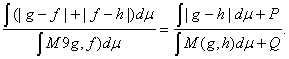 (10)
(10)