«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
М.: МЗ-Пресс, 2004. Глава 3. Статистика нечисловых данных конкретных видов 3.2. Теория случайных толерантностей В прикладных исследованиях обычно используют три конкретных вида бинарных отношений – ранжировки, разбиения и толерантности. Статистические теории ранжировок [7] и разбиений [8] достаточно сложны с математической точки зрения. Поэтому продвинуться удается не очень далеко. Теория случайных ранжировок, в частности, изучает в основном равномерные распределения на множестве ранжировок. Теория случайных толерантностей позволяет рассмотреть принципиально более общие ситуации. Это объясняется, грубо говоря, тем, что для теории толерантностей оказываются полезными суммы некоторых независимых случайных величин, а для теории ранжировок и разбиений аналогичные случайные величины зависимы, а потому изучние их сумм затруднено. Теория случайных толерантностей является частным случаем теории люсианов, рассматриваемой в разделе 3.4. Здесь приводим результаты, специфичные именно для толерантностей. Пусть X - конечное множество из k элементов. Толерантность А на множестве Х, как и любое бинарное отношение, однозначно описывается матрицей ||a(i, j)||, 1 < i, j < k, где a(i, j) = 1, если элементы с номерами i и jсвязаны отношением толерантности, и a(i, j) = 0 в противном случае. Поскольку толерантность – это рефлексивное и симметричное бинарное отношение, то достаточно рассматривать часть матрицы, лежащую над главной диагональю: ||a(i, j), 1 < i<j < k||. Между наборами ||a(i, j), 1 < i<j < k|| из 0 и 1 и толерантностями на Х имеется взаимнооднозначное соответствие. Пусть А = А(ω) – случайная толерантность, равномерно распределенная на множестве всех толерантностей на Х. Легко видеть, что в этом случае a(i, j), 1 < i<j < k, - независимые случайные величины, принимающие значения 0 и 1 с вероятностями 0,5. Этот факт, несмотря на свою математическую тривиальность, является решающим для построения базовой части теории толерантностей. Для аналогичных постановок в теории ранжировок и разбиений величины a(i, j) оказываются зависимыми. Следовательно, случайная величина
имеет биномиальное распределение с параметрами k(k-1)/2, Ѕ и асимптотически нормальна при k → ∞. Проверка гипотез о согласованности. Рассмотрим s независимых толерантностей А1, А2, …, Аs, равномерно распределенных на множестве всех толерантностей на Х. Рассмотрим вектор
где d(Ap, Aq) – расстояние между толерантностями Ap и Aq, аксиоматически введенное в главе 1. В (1) предполагается, что пары (p, q), p < q, располагаются в раз навсегда установленном порядке, для определенности в лексиграфическом (т.е. пары упорядочиваются в соответствии со значением р, а при одинаковых р – по значению q). Вектор ξks является суммой k(k-1)/2 независимых одинаково распределенных случайных векторов, а потому асимптотически нормален при k → ∞. Координаты этого вектора независимы, поскольку, как нетрудно видеть, координаты каждого слагаемого независимы (это свойство не сохраняется при отклонении от равномерности распределения). Распределения случайных величин ap(i, j) и |ap(i, j) - aq(i, j)| совпадают, поэтому распределения В(А) и d(Ap, Aq) также совпадают. В силу многомерной центральной предельной теоремы (приложение 1) распределение вектора
сходится при k → ∞ к распределению многомерного нормального вектора ηs, ковариационная матрица которого совпадает с ковариационной матрицей вектора ηks, а математическое ожидание равно 0. Таким образом, координаты случайного вектора ηs независимы и имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1. В соответствии с теоремами о наследовании сходимости (см. приложение 1) распределение f(ηks) сходится при k → ∞ к распределению f(ηs) для достаточно широкого класса функций f, в частности, для всех непрерывных функций. В качестве примеров рассмотрим статистики
При k → ∞ распределения случайных величин
сходятся соответственно к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1 и распределению хи-квадрат с s(s – 1)/2 степенями свободы. Статистики W и N могут быть использованы для проверки гипотезы о равномерности распределения толерантностей. Как известно, в теории ранговой корреляции [7], т.е. в теории случайных ранжировок, в качестве единой выборочной меры связи нескольких признаков используется коэффициент согласованности W(R), называемый также коэффициентом конкордации [9, табл.6.10]. Его распределение затабулировано в предположении равномерности распределения на пространстве ранжировок (без связей). Непосредственным аналогом W(R) в случае толерантностей является статистика W. Статистики W и N играют ту же роль для толерантностей, что W(R) для ранжировок, однако математико-статистическая теория в случае толерантностей гораздо проще, чем для ранжировок. Обобщением равномерно распределенных толерантностей являются толерантности с независимыми связями. В этой постановке предполагается, что a(i, j), 1 < i<j < k, - независимые случайные величины, принимающие значения 0 и 1. Обозначим Р(a(i, j) = 1) = р(i,j). Тогда Р(a(i, j) = 0) = 1 - р(i,j). Таким образом, распределение толерантности с независимыми связями задается нечеткой толерантностью, т.е. вектором P = {р(i, j), 1 < i<j < k}. Пусть имеется s независимых случайных толерантностей А1, А2, …, Аs с независимыми связями, распределения которых задаются векторами Р1, Р2, …, Рs соответственно. Рассмотрим проверку гипотезы согласованности Н0: Р1 = Р2 =…= Рs. Она является более слабой, чем гипотеза равномерности : Р1 = Р2 =…= Рs =(Ѕ, Ѕ, ..., Ѕ), для проверки которой используют статистики W и N (см. выше). Пусть сначала s = 2. Тогда P{|a1(i, j) - a2(i, j)| = 1} = q(i, j), P{|a1(i, j) - a2(i, j)| = 0} = 1 - q(i, j), где q(i, j) = p1(i, j) (1 - p2(i, j)) + p2(i, j) (1 - p1(i, j)). Следовательно, расстояние d(A1, A2) между двумя случайными толерантностями с независимыми связями есть суммаk(k - 1)/2 независимых случайных величин, принимающих значения 0 и 1, причем математическое ожидание и дисперсия d(A1, A2) таковы:
Пусть k → ∞. Если Dd(A1, A2) → ∞, то условие Линденберга Центральной Предельной Теоремы теории вероятностей выполнено (см. приложение 1), и распределение нормированного расстояния
сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Если существует число δ > 0 такое, что при всех k, i, j, 1 < i<j < k, вероятности p1(i, j) и p2(i, j) лежат внутри интервала (δ; 1 – δ), то Dd(A1, A2) → ∞. Соотношения (2), (3) и им подобные позволяют рассчитать мощность критериев, основанных на статистиках W иN, при k → ∞, подобно тому, как это сделано в [1, глава 4.5]. Поскольку подобные расчеты не требуют новых идей, не будем приводить их здесь. Обычно Р1 и Р2 неизвестны. Для проверки гипотезы Р1 = Р2 в некоторых случаях можно порекомендовать отвергать гипотезу на уровне значимости α, если d(A1, A2) > d0, где d0 есть (1 - α)-квантиль распределения расстояния между двумя независимыми равномерно распределенными случайными толерантностями, т.е. квантиль биномиального распределения В(А). Укажем достаточные условия такой рекомендации. Пусть р =(p1(i, j) + p2(i, j))/2, p1(i, j) = р + Δ, тогда p2(i, j) = р – Δ, q= q(i, j) = 2р(1 – р) + 2Δ2. (4) Если существует число δ > 0 такое, что q – Ѕ > δ > 0 (5) при всех k, i, j, то гипотеза Р1 = Р2 будет отвергаться с вероятностью, стремящейся к 1 при k → ∞. Из (4) следует, что при фиксированном р существует Δ такое, что выполнено (5), тогда и только тогда, когда 0,25 < p < 0,75. Своеобразие постановки задачи проверки гипотезы состоит в том, что при росте k число неизвестных параметров, т.е. координат векторов Pi, растет пропорционально объему данных. Поэтому и столь далекая от оптимальности процедура, как описанная в двух предыдущих абзацах, представляет некоторый практический интерес. Для случая s > 4 в теории люсианов (глава 3.4) разработаны методы проверки гипотезы согласованности Н0: Р1 = Р2=…= Рs. Нахождение группового мнения. Пусть А1, А2, …, Аs - случайные толерантности, описывающие мнения sэкспертов. Для нахождения группового мнения будем использовать медиану Кемени, т.е. эмпирическое среднее относительно расстояния Кемени, введенного в главе 1. Медианой Кемени является
Легко видеть, что Аср = ||aср(i, j)|| удовлетворяет условию: aср(i, j) = 1, если
и aср(i, j) = 0, если
Следовательно, при нечетном s групповое мнение Аср определяется однозначно. При четном s неоднозначность возникает в случае
Тогда медиана Кемени Аср - не одна толерантность, а множество толерантностей, минимум суммы расстояний достигается и при aср(i,j) = 1, и при aср(i, j) = 0. Асимптотическое поведение группового мнения (медианы Кемени для толерантностей) вытекает из общих результатов о законах больших чисел в пространствах произвольной природы (глава 2), поэтому рассматривать его здесь нет необходимости. Дихотомические (бинарные) признаки в классической асимптотике. Многое в предыдущем изложении определялось спецификой толерантностей. В частности, особая роль равномерности распределения на множестве всех толерантностей оправдывала специальное рассмотрение статистик W и N; аксиоматически введенное расстояние dмежду толерантностями играло важную роль в приведенных выше результатах. Однако модель толерантностей с независимыми связями уже меньше связана со спецификой толерантностей. В ней толерантности можно рассматривать просто как частный случай люсианов. Широко применяется следующая модель порождения данных. Пусть А1, А2, …, Аs - независимые люсианы. Это значит, что статистические данные имеют вид (А1, А2, …, Аs) = ||Xij, i = 1,2, ..., s; j = 1, 2, ..., k||, (6) где Xij - независимые в совокупности испытания Бернулли с вероятностями успеха (Р1, Р2, …, Рs) = ||pij, , i = 1,2, ..., s; j = 1, 2, ..., k||, (7) где Pi - вектор вероятностей, описывающий распределение люсиана Ai. Особое значение имеют одинаково распределенные люсианы, для которых Р1 = Р2 =…= Рs = Р, где символом Р обозначен общий вектор вероятностей. Как обычно в математической статистике, содержательные результаты при изучении модели (6) - (7) можно получить в асимптотических постановках. При этом есть два принципиально разных предельных перехода: s → ∞ и k → ∞. Первый из них - традиционный: число неизвестных параметров постоянно, объем выборки s растет. Во втором число параметров растет, объем выборки остается постоянным, но общий объем данных ks растет пропорционально числу неизвестных параметров. Аналогом является асимптотическое изучение коэффициентов ранговой корреляции Кендалла и Спирмена: число ранжировок, т.е. объем выборки, постоянно (и равно 2), а число ранжируемых объектов растет. Вторая постановка изучается в разделе 3.4, посвященном люсианам. Некоторые задачи в первой постановке рассмотрим здесь. Случайные толерантности используются, в частности, для оценки нечетких толерантностей [1]. Для описания результатов опроса группы экспертов о сходстве объектов строят нечеткую толерантность M = ||μij||, μij = lij/nij, где nij - число ответов о сходстве i-го и j-го объектов, а lij - число положительных ответов из них. Если эксперты действуют в соответствии с единым вектором параметров Р, то М - состоятельная оценка для Р. Следующий вопрос при таком подходе - верно ли, что две группы экспертов «думают одинаково», т.е. используют совпадающие вектора Р? Рассмотрим эту постановку на более общем языке люсианов. Пусть A1, A2, ..., Am и B1, B2, ..., Bn - две группы независимых в совокупности люсианов, одинаково распределенные в каждой группе с параметрами Р(А) и Р(В) соответственно. Требуется проверить гипотезу Р(А) =Р(В). Естественным является переход к пределу при min(m, n) → ∞. Пусть гипотеза справедлива. Предположим, что pi = pi(A) = pi(B) ≠ 0 при всех i = 1, 2, ..., k. (Разбор последствий нарушений этого условия оставляем читателю.) Пусть si - число единиц на i-м месте в первой группе люсианов, а ti - во второй. Рассмотрим случайные величины
Они независимы в совокупности. В соответствии с приведенными в приложении 1 предельными теоремами распределения случайных величин ξi при min(m, n) → ∞ сходятся к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Эти свойства сохраняются при замене pi в (8) на состоятельные оценки, построенные по статистическим данным, соответствующим i-му месту. Будем использовать эффективную оценку [10, с.529]
Подставим (9) в (8), получим статистики
Полученные статистики можно использовать для проверки рассматриваемой гипотезы, например, с помощью критериев, основанных на статистиках
С помощью результатов приложения 1 получаем, что W имеет в пределе при min(m, n) → ∞ стандартное нормальное распределение, а Т - распределение хи-квадрат с k степенями свободы. Рассмотрим распределение статистики W при альтернативных гипотезах. Положим
Эти случайные величины независимы, распределение каждой из них при min(m, n) → ∞ сходится к стандартному нормальному распределению. Поскольку
то
где
и
В силу результатов приложения 1 распределение F при min(m, n) → ∞ сближается с нормальным распределением, математическое ожидание которого равно 0, а дисперсия
Поэтому, чтобы получить собственное (т.е. невырожденное) распределение W при альтернативах, естественно рассмотреть модель
где θi - некоторые фиксированные числа. Тогда при min(m, n) → ∞ оценки
и единичной дисперсией. Если в последней формуле θ0 = 0, то асимптотическое распределение W таково же, как и в случае справедливости нулевой гипотезы. От указанного недостатка свободна статистика Т. Тем же путем, как и для W, получаем, что при min(m, n) → ∞ распределение Т сходится к нецентральному хи-квадрат распределению с kстепенями свободы и параметром нецентральности
Можно рассматривать ряд других задач, например, проверку совпадения параметров для нескольких групп люсианов (аналог дисперсионного анализа), установление зависимости Р(В) от Р(А) (аналог регрессионного анализа), отнесение вновь поступающего люсиана к одной из групп (речь идет о задаче диагностики - аналоге дискриминантного анализа; она представляет интерес, например, при применении тестов типа MMPI оценки психического состояния личности) и т.д. Однако принципиальных трудностей на пути развития соответствующих методов не видно, и мы не будем их здесь рассматривать. Создание соответствующих алгоритмов проводится специалистами по прикладной статистике в соответствии с непосредственными заказами пользователей.
|
||
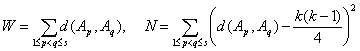 .
.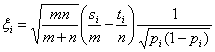 . (8)
. (8)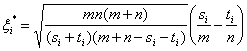 .
.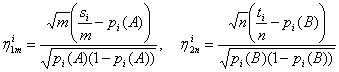 .
.