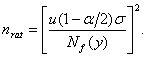«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
М.: МЗ-Пресс, 2004. Глава 4. Статистика интервальных данных 4.3. Интервальные данные в задачах проверки гипотез С позиций статистики интервальных данных целесообразно изучить все практически используемые процедуры прикладной математической статистики, установить соответствующие нотны и рациональные объемы выборок. Это позволит устранить разрыв между математическими схемами прикладной статистики и реальностью влияния погрешностей наблюдений на свойства статистических процедур. Статистика интервальных данных – часть теории устойчивых статистических процедур, развитой в монографии [3]. Часть, более адекватная реальной статистической практике, чем некоторые другие постановки, например, с засорением нормального распределения большими выбросами. Рассмотрим подходы статистики интервальных данных в задачах проверки статистических гипотез. Пусть принятие решения основано на сравнении рассчитанного по выборке значения статистики критерия Пример 1. Пусть Как известно из любого учебного курса математической статистики, следует использовать следует использовать статистику При ограничениях (1) на абсолютную погрешность Если же n = 400 при Вернемся к общему случаю проверки гипотез. С учетом погрешностей измерений граничное значение
Если f = |f1|, где f1 при справедливости H0 имеет асимптотически нормальное распределение с математическим ожиданием 0 и дисперсией
при больших n, где
В условиях примера 1
Пример 2. Рассмотрим статистику одновыборочного критерия Стьюдента
где v – выборочный коэффициент вариации. Тогда с точностью до бесконечно малых более высокого порядка нотна для t имеет вид
где Nv(y) – рассмотренная ранее нотна для выборочного коэффициента вариации. Поскольку распределение статистики Стьюдента t сходится к стандартному нормальному, то небольшое изменение предыдущих рассуждений дает
Пример 3. Рассмотрим двухвыборочный критерий Смирнова, предназначенный для проверки однородности (совпадения) функций распределения двух независимых выборок [41]. Статистика этого критерия имеет вид
где Fm(x) – эмпирическая функция распределения, построенная по первой выборке объема m, извлеченной из генеральной совокупности с функцией распределения F(x), а Gn(x) – эмпирическая функция распределения, построенная по второй выборке объема n, извлеченной из генеральной совокупности с функцией распределения G(x). Нулевая гипотеза имеет вид При ограничениях (1) на абсолютные погрешности и справедливости нулевой гипотезы
Если F(x)=G(x)=x при 0<x<1, то
Правая часть этой формулы при Теоретические результаты в области статистических методов входят в практику через алгоритмы расчетов, воплощенные в программные средства (пакеты программ, диалоговые системы). Ввод данных в современном статистической программной системе должен содержать запросы о погрешностях результатов измерений. На основе ответов на эти запросы вычисляются нотны рассматриваемых статистик, а затем – доверительные интервалы при оценивании, разброс уровней значимости при проверке гипотез, рациональные объемы выборок. Необходимо использовать систему алгоритмов и программ статистики интервальных данных, «параллельную» подобным системам для классической математической статистики.
|
||