«Управление и Оптимизация Производственного Предприятия»
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
М.: МЗ-Пресс, 2004. Глава 1. Нечисловые статистические данные 1.5. Нечеткие множества – частный случай нечисловых данных Уже много раз упоминались нечеткие множества как практически важный вид объектов нечисловой природы. Что же это такое? Познакомимся с основами теории нечетких множеств. Нечеткие множества. Пусть A - некоторое множество. Подмножество B множества A характеризуется своей характеристической функцией
Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество C множества A характеризуется своей функцией принадлежности Если функция принадлежности Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений. Теория нечеткости является обобщением интервальной математики. Действительно, функция принадлежности
задает интервальную неопределенность – про рассматриваемую величину известно лишь, что она лежит в заданном интервале [a,b]. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов. Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А.Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ. Первая книга российского автора по теории нечеткости вышла в 1980 г. [24]. Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятиями, качеством продукции и технологическими процессами, при описании предпочтений потребителей и оптимизации процессов варки стали. Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный. Аппарат теории нечеткости громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть C и D - два нечетких подмножества A с функциями принадлежности
соответственно. Как уже отмечалось, теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Соответствующий цикл теорем приведен в следующем разделе. Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные. Для знакомства со спецификой нечетких множеств изучим некоторые их свойства. В дальнейшем считаем, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества Y. Законы де Моргана для нечетких множеств. Как известно, законами же Моргана называются следующие тождества алгебры множеств
Теорема 1. Для нечетких множеств справедливы тождества
Доказательство теоремы 1 состоит в непосредственной проверке справедливости соотношений (3) и (4) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных выше. Тождества (3) и (4) назовем законами де Моргана для нечетких множеств. В отличие от классического случая соотношений (2), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношение (2) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания. Дистрибутивный закон для нечетких множеств. Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так, Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что "не всегда". Внесем полную ясность. Теорема 2. Для любых нечетких множеств А, В и С
В то же время равенство
справедливо тогда и только тогда, когда при всех
Доказательство. Фиксируем произвольный элемент
Рассмотрим различные упорядочения трех чисел a, b, c. Пусть сначала Пусть Если Три остальные упорядочения чисел a, b, c разбирать нет необходимости, поскольку в соотношение (6) числа b иc входят симметрично. Тождество (5) доказано. Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами
и
Эти два выражения совпадают тогда и только тогда, когда, когда Определение 1. Носителем нечеткого множества А называется совокупность всех точек Следствие теоремы 2. Если носители нечетких множеств В и С совпадают с У, то равенство (6) имеет место тогда и только тогда, когда А - "четкое" (т.е. обычное, классическое, не нечеткое) множество. Доказательство. По условию Пример описания неопределенности с помощью нечеткого множества. Понятие «богатый» часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики провели в 2004 г. небольшое пилотное (т.е пробное) социологическое исследование представления различных слоёв населения о понятии "богатый человек". Мини-анкета опроса выглядела так: 1. При каком месячном доходе (в тыс. руб. на одного человека) Вы считали бы себя богатым человеком? 2. Оценив свой сегодняшний доход, к какой из категорий Вы себя относите: а) богатые; б) достаток выше среднего; в) достаток ниже среднего; г) бедные; д) за чертой бедности? (В дальнейшем вместо полного наименования категорий будем оперировать буквами, например "в" - категория, "б" - категория и т.д.) 3. Ваша профессия, специальность. Всего было опрошено 74 человека, из них 40 - научные работники и преподаватели, 34 человека - не занятых в сфере науки и образования, в том числе 5 рабочих и 5 пенсионеров. Из всех опрошенных только один (!) считает себя богатым. Несколько типичных ответов научных работников и преподавателей приведено в табл.1, а аналогичные сведения для работников коммерческой сферы – в табл.2. Таблица 1. Типичные ответы научных работников и преподавателей
Таблица 2 Типичные ответы работников коммерческой сферы.
Разброс ответов на первый вопрос – от 6 до 600 тыс. руб. в месяц на человека. Результаты опроса показывают, что критерий богатства у финансовых работников в целом несколько выше, чем у научных работников и преподавателей (см. гистограммы на рис.1 и рис.2 ниже). Опрос показал, что выявить какое-нибудь конкретное значение суммы, которая необходима "для полного счастья", пусть даже с небольшим разбросом, нельзя, что вполне естественно. Как видно из таблиц 1 и 2, денежный эквивалент богатства колеблется от 6 до 600 тысяч рублей в месяц. Подтвердилось мнение, что работники сферы образования в подавляющем большинстве причисляют свой достаток к категории "в" и ниже (81% опрошенных), в том числе к категории "д" отнесли свой достаток 57%. Со служащими коммерческих структур и бюджетных организаций иная картина: "г" - категория 1 человек (4%), "д" - категория 4 человека (17%), "б" - категория - 46% и 1 человек "а" - категория. Пенсионеры, что не вызывает удивления, отнесли свой доход к категории "д" (4 человека), и лишь один человек указал "г" - категорию. Рабочие же ответили так: 4 человека - "в", и один человек - "б". Для представления общей картины в табл.3 приведены данные об ответах работников других профессий. Таблица 3. Типичные ответы работников различных профессий.
Прослеживается интересное явление: чем выше планка богатства для человека, тем к более низкой категории относительно этой планки он себя относит. Для сводки данных естественно использовать гистограммы. Для этого необходимо сгруппировать ответы. Использовались 7 классов (интервалов): 1 – до 30 тысяч рублей в месяц на человека (включительно); 2 – от 30 до 60 тысяч; 3- от 60 до 90 тысяч; 4 – от 90 до 120 тысяч; 5 – от 120 до 150 тысяч; 6 – от 150 до 180 тысяч; 7 – более 180 тысяч. (Во всех интервалах левая граница исключена, а правая, наоборот – включена.) Сводная информация представлена на рис.1 (для научных работников и преподавателей) и рис.2 (для всех остальных, т.е. для лиц, не занятых в сфере науки и образования - служащих иных бюджетных организаций, коммерческих структур, рабочих, пенсионеров).
Рис.1. Гистограмма ответов на вопрос 1 для научных работников и преподавателей (40 человек).
Рис.2. Гистограмма ответов на вопрос 1 для лиц, не занятых в сфере науки и образования (34 человека). Для двух выделенных групп, а также для некоторых подгрупп второй группы рассчитаны сводные средние характеристики – выборочные средние арифметические, медианы, моды. При этом медиана группы - количество млн. руб., названное центральным по порядковому номеру опрашиваемым в возрастающем ряду ответов на вопрос 1, а мода группы - интервал, на котором столбик гистограммы - самый высокий, т.е. в него "попало" максимальное количество опрашиваемых. Результаты приведены в табл. 4. Таблица 4. Сводные средние характеристики ответов на вопрос 1 для различных групп (в тыс. руб. в мес. на чел.).
Построим нечеткое множество, описывающее понятие «богатый человек» в соответствии с представлениями опрошенных. Для этого составим табл.5 на основе рис.1 и рис.2 с учетом размаха ответов на первый вопрос. Таблица 5. Число ответов, попавших в интервалы
Пятая строка табл.5 задает функцию принадлежности нечеткого множества, выражающего понятие "богатый человек" в терминах его ежемесячного дохода. Это нечеткое множество является подмножеством множества из 9 интервалов, заданных в строке 2 табл.5. Или множества из 9 условных номеров {0, 1, 2, …, 8}. Эмпирическая функция распределения, построенная по выборке из ответов 74 опрошенных на первый вопрос мини-анкеты, описывает понятие "богатый человек" как нечеткое подмножество положительной полуоси. О разработке методики ценообразования на основе теории нечетких множеств. Для оценки значений показателей, не имеющих количественной оценки, можно использовать методы нечетких множеств. Например, в диссертации П.В. Битюкова [26] нечеткие множества применялись при моделировании задач ценообразования на электронные обучающие курсы, используемые при дистанционном обучении. Им было проведено исследование значений фактора «Уровень качества курса» с использованием нечетких множеств. В ходе практического использования предложенной П.В. Битюковым методики ценообразования значения ряда других факторов могут также определяться с использованием теории нечетких множеств. Например, ее можно использовать для определения прогноза рейтинга специальности в вузе с помощью экспертов, а также значений других факторов, относящихся к группе «Особенности курса». Опишем подход П.В. Битюкова как пример практического использования теории нечетким множеств. Значение оценки, присваиваемой каждому интервалу для фактора «Уровень качества курса», определяется на универсальной шкале [0;1], где необходимо разместить значения лингвистической переменной «Уровень качества курса»: НИЗКИЙ, СРЕДНИЙ, ВЫСОКИЙ. Степень принадлежности некоторого значения вычисляется как отношение числа ответов, в которых оно встречалось в определенном интервале шкалы, к максимальному (для этого значения) числу ответов по всем интервалам. Был проведен опрос экспертов о степени влияния уровня качества электронных курсов на их потребительную ценность. Каждому эксперту в процессе опроса предлагалось оценить с позиции потребителя ценность того или иного класса курсов в зависимости от уровня качества. Эксперты давали свою оценку для каждого класса курсов по 10-ти балльной шкале (где 1 - min, 10 - max). Для перехода к универсальной шкале [0;1], все значения 10-ти балльной шкалы оценки ценности были разделены на максимальную оценку, т.е. на 10. Используя свойства функции принадлежности, необходимо предварительно обработать данные с тем, чтобы уменьшить искажения, вносимые опросом. Естественными свойствами функций принадлежности являются наличие одного максимума и гладкие, затухающие до нуля фронты. Для обработки статистических данных можно воспользоваться так называемой матрицей подсказок. Предварительно удаляются явно ошибочные элементы. Критерием удаления служит наличие нескольких нулей в строке вокруг этого элемента. Элементы матрицы подсказок вычисляются по формуле: где
Для столбцов, где
Результаты расчетов сводятся в таблицу, на основании которой строятся функции принадлежности. Для этого находятся максимальные элементы по строкам:
Функция принадлежности вычисляется по формуле: Таблица 6 Значения функции принадлежности лингвистической переменной
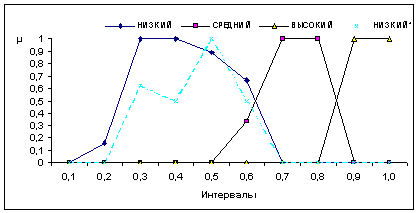
На рис.3 сплошными линиями показаны функции принадлежности значений лингвистической переменной «Уровень качества курса» после обработки таблицы, содержащей результаты опроса. Как видно из графика, функции принадлежности удовлетворяют описанным выше свойствам. Для сравнения пунктирной линией показана функция принадлежности лингвистической переменной для значения НИЗКИЙ без обработки данных.
Рис. 3. График функций принадлежности значений лингвистической переменной «Уровень качества курса»
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
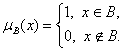 (1)
(1)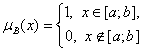
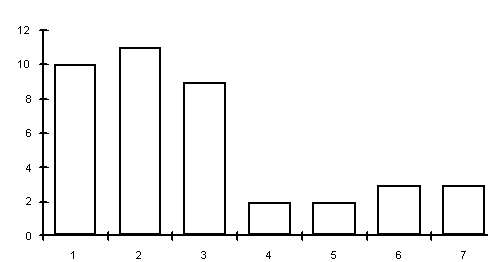
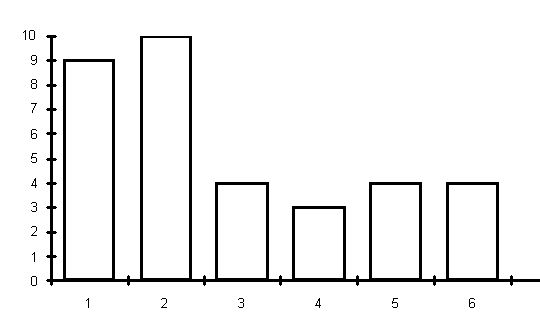
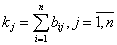 ,
,