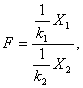«Управление и Оптимизация Производственного Предприятия»

Распределения Пирсона (хи – квадрат), Стьюдента и Фишера

С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.

Распределение Пирсона (хи - квадрат) – распределение случайной величины

где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных [8, 9, 11, 16].

Распределение t Стьюдента – это распределение случайной величины

где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X– распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

Распределение Стьюдента было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.

В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д. [8, 9, 11, 16].

Распределение Фишера – это распределение случайной величины

где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂ – число степеней свободы знаменателя. Распределение случайной величины Fназвано в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.

Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики [8, 9, 11, 16].

Выражения для функций распределения хи - квадрат, Стьюдента и Фишера, их плотностей и характеристик, а также таблицы, необходимые для их практического использования, можно найти в специальной литературе (см., например, [8]).