«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Математика случая Вероятность и статистика – основные факты Учебное пособие. М.: МЗ-Пресс, 2004. 5. Основные проблемы прикладной статистики - описание данных, оценивание и проверка гипотез Доверительное оценивание Какова точность оценки параметра? В каких границах он может лежать? В научных публикациях и учебной литературе, в нормативно-технической и инструктивно-методической документации, в таблицах и программных продуктах наряду с алгоритмами расчетов точечных оценок даются правила нахождения доверительных границ. Они и указывают точность точечной оценки. При этом используются такие термины, как доверительная вероятность, доверительный интервал. Если речь идет об оценивании нескольких числовых параметров, или же функции, упорядочения и т.п., то говорят об оценивании с помощью доверительной области. Доверительная область – это область в пространстве параметров, в которую с заданной вероятностью входит неизвестное значение оцениваемого параметра распределения. «Заданная вероятность» называется доверительной вероятностью и обычно обозначается γ. Пусть Θ – пространство параметров. Рассмотрим статистику Θ1 = Θ1(x1, x2,…, xn) – функцию от результатов наблюдений x1, x2,…, xn, значениями которой являются подмножества пространства параметров Θ. Так как результаты наблюдений – случайные величины, то Θ1 – также случайная величина, значения которой – подмножества множества Θ, т.е. Θ1 – случайное множество. Напомним, что множество – один из видов объектов нечисловой природы, случайные множества изучают в теории вероятностей и статистике объектов нечисловой природы. В ряде литературных источников, к настоящему времени во многом устаревших, под случайными величинами понимают только те из них, которые в качестве значений принимают действительные числа. Согласно справочнику академика РАН Ю.В.Прохорова и проф. Ю.А.Розанова [12] случайные величины могут принимать значения из любого множества. Так, случайные вектора, случайные функции, случайные множества, случайные ранжировки (упорядочения) – это отдельные виды случайных величин. Используется и иная терминология: термин «случайная величина» сохраняется только за числовыми функциями, определенными на пространстве элементарных событий, а в случае иных областей значений используется термин «случайный элемент». (Замечание для математиков: все рассматриваемые функции, определенные на пространстве элементарных событий, предполагаются измеримыми.) Статистика Θ1 называется доверительной областью, соответствующей доверительной вероятности γ, если
Ясно, что этому условию удовлетворяет, как правило, не одна, а много доверительных областей. Из них выбирают для практического применения какую-либо одну, исходя из дополнительных соображений, например, из соображений симметрии или минимизируя объем доверительной области, т.е. меру множества Θ1. При оценке одного числового параметра в качестве доверительных областей обычно применяют доверительные интервалы (в том числе лучи), а не иные типа подмножеств прямой. Более того, для многих двухпараметрических и трехпараметрических распределений (нормальных, логарифмически нормальных, Вейбулла-Гнеденко, гамма-распределений и др.) обычно используют точечные оценки и построенные на их основе доверительные границы для каждого из двух или трех параметров отдельно. Это делают для удобства пользования результатами расчетов: доверительные интервалы легче применять, чем фигуры на плоскости или тела в трехмерном пространстве. Как следует из сказанного выше, доверительный интервал – это интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения. Границы доверительного интервала называютдоверительными границами. Доверительная вероятность γ – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным. Оцениванием с помощью доверительного интервала называют способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала. Для числового параметра θ рассматривают верхнюю доверительную границу θВ, нижнюю доверительную границу θН и двусторонние доверительные границы – верхнюю θ1В и нижнюю θ1Н. Все четыре доверительные границы – функции от результатов наблюдений x1, x2,…, xn и доверительной вероятности γ. Верхняя доверительная граница θВ – случайная величина θВ = θВ(x1, x2,…, xn; γ), для которой Р(θ<θВ) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид (-∞; θВ]. Нижняя доверительная граница θН – случайная величина θН = θН(x1, x2,…, xn; γ), для которой Р(θ>θH) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид [θH; +∞). Двусторонние доверительные границы - верхняя θ1В и нижняя θ1Н - это случайные величины θ1В = θ1В(x1, x2,…, xn; γ) и θ1Н = θ1Н(x1, x2,…, xn; γ) такие, что Р(θ1H<θ<θ1В) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид [θ1H; θ1В]. Вероятности, связанные с доверительными границами, можно записать в виде частных случаев формулы (5):
В нормативно-технической и инструктивно-методической документации, научной и учебной литературе используют два типа правил определения доверительных границ – построенных на основе точного распределения и построенных на основе асимптотического распределения некоторой точечной оценки θn параметра θ. Рассмотрим примеры. Пример 10. Пусть x1, x2,…, xn – выборка из нормального закона N(m, σ), параметры m и σ неизвестны. Укажем доверительные границы для m. Известно [11], что случайная величина
имеет распределение Стьюдента с (т-1) степенью свободы, где P{Y < tγ(n-1)} = γ, P{Y > t1-γ(n-1)} = γ. Следовательно,
т.е. в качестве нижней доверительной границы θН, соответствующей доверительной вероятности γ, следует взять
Аналогично получаем, что
Поскольку распределение Стьюдента симметрично относительно 0, то
Как построить двусторонние доверительные границы? Положим
где θ1Н и θ1В заданы формулами (6) и (7) соответственно. Поскольку неравенство θ1Н < m < θ1В выполнено тогда и только тогда, когда
то P{θ1H < m < θ1B} = γ1 + γ2 - 1, (в предположении, что γ1 > 0,5; γ2 > 0,5). Следовательно, если γ = γ1 + γ2 – 1, то θ1Н и θ1В – двусторонние доверительные границы для m, соответствующие доверительной вероятности γ. Обычно полагают γ1 = γ2, т.е. в качестве двусторонних доверительных границ θ1Н и θ1В, соответствующих доверительной вероятности γ, используют односторонние доверительные границы θН и θВ, соответствующие доверительной вероятности (1+γ)/2. Другой вид правил построения доверительных границ для параметра θ основан на асимптотической нормальности некоторой точечной оценки θn этого параметра. В вероятностно-статистических методах принятия решений используют, как уже отмечалось, несмещенные или асимптотически несмещенные оценки θn, для которых смещение либо равно 0, либо при больших объемах выборки пренебрежимо мало по сравнению со средним квадратическим отклонением оценки θn. Для таких оценок при всех х
где Ф(х) – функция нормального распределения N(0;1). Пусть uγ – квантиль порядка γ распределения N(0;1). Тогда
Поскольку неравенство
равносильно неравенству
то в качестве θН можно было бы взять левую часть последнего неравенства. Однако точное значение дисперсии D(θn) обычно неизвестно. Зато часто удается доказать, что дисперсия оценки имеет вид
(с точностью до пренебрежимо малых при росте n слагаемых), где h(θ) – некоторая функция от неизвестного параметра θ. Справедлива теорема о наследовании сходимости [7, §2.4], согласно которой при подстановке в h(θ) оценки θn вместо θ соотношение (8) остается справедливым, т.е.
Следовательно, в качестве приближенной нижней доверительной границы следует взять
а в качестве приближенной верхней доверительной границы -
С ростом объема выборки качество приближенных доверительных границ улучшается, т.к. вероятности событий {θ >θH} и {θ <θB} стремятся к γ. Для построения двусторонних доверительных границ поступают аналогично правилу, указанному выше в примере 10 для интервального оценивания параметра m нормального распределения. А именно, используют односторонние доверительные границы, соответствующие доверительной вероятности (1+γ)/2. При обработке экономических, управленческих или технических статистических данных обычно используют значение доверительной вероятности γ = 0,95. Применяют также значения γ = 0,99 или γ = 0,90. Иногда встречаются значения γ = 0,80, γ = 0,975, γ = 0,98 и др.
|
||
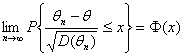 ,
,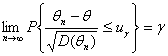 (8)
(8)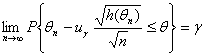 .
.