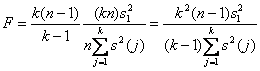«Управление и Оптимизация Производственного Предприятия»

Дисперсионный анализ

Дисперсионный анализ применяют для изучения влияния качественных признаков на количественную переменную. Например, пусть имеются k выборок результатов измерений количественного показателя качества единиц продукции, выпущенных на k станках, т.е. набор чисел (x₁(j), x₂(j), … , x_n(j)), где j – номер станка, j = 1, 2, …, k, а n – объем выборки. В распространенной постановке дисперсионного анализа предполагают, что результаты измерений независимы и в каждой выборке имеют нормальное распределение N(m(j), σ²) с одной и той же дисперсией. Хорошо разработаны и непараметрические постановки [19].

Проверка однородности качества продукции, т.е. отсутствия влияния номера станка на качество продукции, сводится к проверке гипотезы

H₀: m(1) = m(2) = … = m(k).

В дисперсионном анализе разработаны методы проверки подобных гипотез. Теория дисперсионного анализа и расчетные формулы рассмотрены в специальной литературе [20].

Гипотезу Н₀ проверяют против альтернативной гипотезы Н₁, согласно которой хотя бы одно из указанных равенств не выполнено. Проверка этой гипотезы основана на следующем «разложении дисперсий», указанном Р.А.Фишером:

(7)

где s² – выборочная дисперсия в объединенной выборке, т.е.

Далее, s²(j) – выборочная дисперсия в j-ой группе,

Таким образом, первое слагаемое в правой части формулы (7) отражает внутригрупповую дисперсию. Наконец, - межгрупповая дисперсия,

Область прикладной статистики, связанную с разложениями дисперсии типа формулы (7), называют дисперсионным анализом. В качестве примера задачи дисперсионного анализа рассмотрим проверку приведенной выше гипотезы Н₀ в предположении, что результаты измерений независимы и в каждой выборке имеют нормальное распределение N(m(j), σ²) с одной и той же дисперсией. При справедливости Н₀ первое слагаемое в правой части формулы (7), деленное на σ², имеет распределение хи-квадрат с k(n-1) степенями свободы, а второе слагаемое, деленное на σ², также имеет распределение хи-квадрат, но с (k-1) степенями свободы, причем первое и второе слагаемые независимы как случайные величины. Поэтому случайная величина

имеет распределение Фишера с (k-1) степенями свободы числителя и k(n-1) степенями свободы знаменателя. ГипотезаН₀ принимается, если F < F_1-α, и отвергается в противном случае, где F_1-α – квантиль порядка 1-α распределения Фишера с указанными числами степеней свободы. Такой выбор критической области определяется тем, что при Н₁величина F безгранично увеличивается при росте объема выборок n. Значения F_1-α берут из соответствующих таблиц [8].

Разработаны непараметрические методы решения классических задач дисперсионного анализа [19], в частности, проверки гипотезы Н₀.