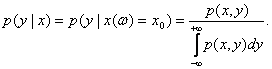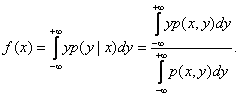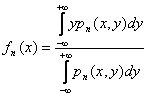«Управление и Оптимизация Производственного Предприятия»
|
|
|
||||||||||||||||||||||||||||||||
|
Эконометрика Учебник. М.: Издательство "Экзамен", 2002. Глава 5. Многомерный статистический анализ 5.2. Основы линейного регрессионного анализа В предыдущем пункте метод наименьших квадратов описан в простейшем случае. Он допускает различные обобщения. Например, метод наименьших квадратов дает алгоритм расчетов в случае, если исходные данные – по-прежнему наборn пар чисел (tk , xk), k = 1,2,…,n, где tk – независимая переменная (например, время), а xk – зависимая (например, индекс инфляции - см. главу 7), а восстанавливать надо не линейную зависимость, а квадратическую:
Следует рассмотреть функцию трех переменных
Оценки метода наименьших квадратов - это такие значения параметров a*, b* и с*, при которых функция f(a,b,с)достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b,с) по аргументам a, b и с, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:
Приравнивая частную производную к 0, получаем линейное уравнение относительно трех неизвестных параметровa,b,c:
Приравнивая частную производную по параметру b к 0, аналогичным образом получаем уравнение
Наконец, приравнивая частную производную по параметру с к 0, получаем уравнение
Решая систему трех уравнений с тремя неизвестными, находим оценки метода наименьших квадратов. Другие задачи, рассмотренные в предыдущем пункте (доверительные границы для параметров и прогностической функции и др.), также могут быть решены. Соответствующие алгоритмы более громоздки. Для их записи полезен аппарат матричной алгебры (см., например, одну из лучших в этой области монографий [2]). Для реальных расчетов используют соответствующие компьютерные программы. Раздел многомерного статистического анализа, посвященный восстановлению зависимостей, называется регрессионным анализом. Термин "линейный регрессионный анализ" используют, когда рассматриваемая функция линейно зависит от оцениваемых параметров (от независимых переменных зависимость может быть произвольной). Теория оценивания неизвестных параметров хорошо развита именно в случае линейного регрессионного анализа. Если же линейности нет и нельзя перейти к линейной задаче, то, как правило, хороших свойств от оценок ожидать не приходится. Продемонстрируем подходы в случае зависимостей различного вида. Если зависимость имеет вид многочлена (полинома)
то коэффициенты многочлена могут быть найдены путем минимизации функции
Функция от t не обязательно должна быть многочленом. Можно, например, добавить периодическую составляющую, соответствующую сезонным колебаниям. Хорошо известно, например, что инфляция (рост потребительских цен) имеет четко выраженный годовой цикл - в среднем цены быстрее всего растут зимой, в декабре - январе, а медленнее всего (иногда в среднем даже падают) летом, в июле - августе. Пусть для определенности
тогда неизвестные параметры могут быть найдены путем минимизации функции
Пусть I(t) -индекс инфляции в момент t. Принцип стабильности условий приводит к гипотезе о постоянстве темпов роста средних цен, т.е. индекса инфляции. Таким образом, естественная модель для индекса инфляции - это
Эта модель не является линейной, метод наименьших квадратов непосредственно применять нельзя. Однако если прологарифмировать обе части предыдущего равенства:
то получим линейную зависимость, рассмотренную в первом пункте настоящей главы. Независимых переменных может быть не одна, а несколько. Пусть, например, по исходным данным
где
Зависимость от х и у не обязательно должна быть линейной. Предположим, что из каких-то соображений известно, что зависимость должна иметь вид
тогда для оценки пяти параметров необходимо минимизировать функцию
Более подробно рассмотрим пример из микроэкономики. В одной из оптимизационных моделей поведения фирмы используется т.н. производственная функция f(K,L), задающая объем выпуска в зависимости от затрат капитала K и труда L. В качестве конкретного вида производственной функции часто используется так называемая функция Кобба-Дугласа
Однако откуда взять значения параметров a и b? Естественно предположить, что они - одни и те же для предприятий отрасли. Поэтому целесообразно собрать информацию
Следовательно, целесообразно сделать замену переменных
а затем находить оценки параметров a и B, минимизируя функцию
Найдем частные производные:
Приравняем частные производные к 0, сократим на 2, раскроем скобки, перенесем свободные члены вправо. Получим систему двух линейных уравнений с двумя неизвестными: Таким образом, для вычисления оценок метода наименьших квадратов необходимо найти пять сумм
Для упорядочения расчета этих сумм может быть использована таблица типа той, что применялась в первом пункте настоящей главы. Отметим, что рассмотренная там постановка переходит в разбираемую сейчас при Подходящая замена переменных во многих случаях позволяет перейти к линейной зависимости. Например, если
то замена z=1/y приводит к линейной зависимости z = a + bx. Если y=(a+bx)2, то замена Основной показатель качества регрессионной модели. Одни и те же данные можно обрабатывать различными способами. Показателем отклонений данных от модели служит остаточная сумма квадратов SS. Чем этот показатель меньше, тем приближение лучше, значит, и модель лучше описывает реальные данные. Однако это рассуждение годится только для моделей с одинаковым числом параметров. Ведь если добавляется новый параметр, по которому можно минимизировать, то и минимум, как правило, оказывается меньше. В качестве основного показателя качества регрессионной модели используют оценку остаточной дисперсии
скорректированную на число m параметров, оцениваемых по наблюдаемым данным. В случае линейной прогностической модели, рассмотренной в первом пункте настоящей главы, оценка остаточной дисперсии имеет вид
поскольку число оцениваемых параметров m=2. Почему эта формула отличается от приведенной в первом пункте? Там в знаменателе n, а здесь - (n-2). Дело в том, что в первом пункте рассмотрена непараметрическая теория при большом объеме данных (при А вот при подборе вида модели знаменатель дроби, оценивающей остаточную дисперсию, приходится корректировать на число параметров. Если этого не делать, то придется заключить, что многочлен второй степени лучше соответствует данным, чем линейная функция, многочлен третьей степени лучше приближает исходные данные, чем многочлен второй степени, и т.д. В конце концов доходим до многочлена степени (n-1) с n коэффициентами, который проходит через все заданные точки. Но его прогностические возможности, скорее всего, существенно меньше, чем у линейной функции. Излишнее усложнение эконометрических моделей вредно. Типовое поведение скорректированной оценки остаточной дисперсии
в зависимости от параметра m в случае расширяющейся системы эконометрических моделей выглядит так. Сначала наблюдаем заметное убывание. Затем оценка остаточной дисперсии колеблется около некоторой константы (теоретического значения дисперсии погрешности). Поясним ситуацию на примере эконометрической модели в виде многочлена
Пусть эта модель справедлива при
Следовательно, скорректированная оценка остаточной дисперсии будет колебаться около указанного предела. Поэтому в качестве оценки неизвестной эконометрику степени многочлена (полинома) можно использовать первый локальный минимум скорректированной оценки остаточной дисперсии, т.е.
В работе [3] найдено предельное распределение этой оценки степени многочлена. Теорема. При справедливости некоторых условий регулярности
где
Таким образом, предельное распределение оценки m* степени многочлена (полинома) является геометрическим. Это означает, в частности, что оценка не является состоятельной. При этом вероятность получить меньшее значение, чем истинное, исчезающе мала. Далее имеем:
Разработаны и иные методы оценивания неизвестной степени многочлена, например, с помощью многократного применения процедуры проверки адекватности регрессионной зависимости с помощью статистики Фишера (см. работу [3]). Предельное поведение оценок - таково же, как в приведенной выше теореме, только значение параметра Линейный и непараметрические парные коэффициенты корреляции. Термин "корреляция" означает "связь". В эконометрике этот термин обычно используется в сочетании "коэффициенты корреляции". Рассмотрим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов
Если rn = 1, то Коэффициенты корреляции типа rn используются во многих алгоритмах многомерного статистического анализа эконометрических данных. В теоретических рассмотрениях часто считают, что случайный вектор имеет многомерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных (см. главу 4). Почему же распространено представление о многомерном нормальном распределении? Дело в том, что теория в этом случае проще. В частности, равенство 0 теоретического коэффициента корреляции (см. приложение 1) эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если Если случайные вектора
(сходимость по вероятности). Более того, выборочный коэффициент корреляции является асимптотически нормальным. Это означает, что
где
Здесь под
(см. приложение 1 в конце книги). Для расчета непараметрического коэффициента ранговой корреляции Спирмена необходимо сделать следующее. Для каждого xi рассчитать его ранг ri в вариационном ряду, построенном по выборке Табл.2. Данные для расчета коэффициентов корреляции
Для данных табл.2 коэффициент линейной корреляции равен 0,83, непосредственной линейной связи нет. А вот коэффициент ранговой корреляции равен 1, поскольку увеличение одной переменной однозначно соответствует увеличению другой переменной. Во многих экономических задачах, например, при выборе инвестиционных проектов для осуществления, достаточно именно монотонной зависимости одной переменной от другой. Поскольку суммы рангов и их квадратов нетрудно подсчитать, то коэффициент ранговой корреляции Спирмена равен
Отметим, что коэффициент ранговой корреляции Спирмена остается постоянным при любом строго возрастающем преобразовании шкалы измерения результатов наблюдений. Другими словами, он является адекватным в порядковой шкале (см. главу 3), как и другие ранговые статистики (см. статистики Вилкоксона, Смирнова, типа омега-квадрат для проверки однородности независимых выборок в главе 4 и общее обсуждение в главе 8). Широко используется также коэффициент ранговой корреляции t Кендалла, коэффициент ранговой конкордации Кендалла и Б. Смита и др. Наиболее подробное обсуждение этой тематики содержится в монографии [6], необходимые для практических расчетов таблицы имеются в справочнике [1]. Дискуссия о выборе вида коэффициентов корреляции продолжается до настоящего времени [5]. Непараметрическая регрессия. Рассмотрим общее понятие регрессии как условного математического ожидания. Пусть случайный вектор
Условное математическое ожидание, т.е. регрессионная зависимость, имеет вид
Таким образом, для нахождения оценок регрессионной зависимости достаточно найти оценки совместной плотности распределения вероятности
при
при
Общий подход к построению непараметрических оценок плотности распределения вероятностей развит в главе 8 ниже.
|
|||||||||||||||||||||||||||||||||