«Управление и Оптимизация Производственного Предприятия»
|
|
|
|||||||||||||||
|
Анализ устойчивости относительно поставленной цели как один из подходов к описанию функционирования организации в условиях неопределенности Монография, Самара, 2001. Глава 3. Моделирование неопределенности Актуальность задач анализа и управления устойчивостью обусловлена непредсказуемостью ситуации, в которой организации предстоит достигать поставленных целей в будущих периодах. Формальный алгоритм анализа и управления устойчивостью для получения численного решения задачи предполагает возможность формализовать, промоделировать неопределенность. Объектом моделирования неопределенности являются события (или совокупности событий). В ходе моделирования неопределенности устанавливается формальная связь между событиями и численными показателями возможности их осуществления. Предварительным этапом для моделирования неопределенности является прогноз значений исследуемого показателя в будущих периодах, получаемый применением математических методов прогнозирования [11, c. 144-175] или экспертных оценок. Наряду с прогнозными значениями исследуемого показателя, которые одновременно являются его ожидаемыми значениями в будущих периодах, т.к. наиболее вероятны с точки зрения исследователя, необходимо получить доверительные интервалы прогнозов, в которых будут находиться реальные значения исследуемого показателя в будущих периодах с заданной вероятностью (надежностью). Доверительные интервалы получают либо применением формальных математических методов [11, c. 155-157], либо экспертными оценками. Для моделирования неопределенности предлагается использовать аппарат теории вероятностей и математической статистики, центральными категориями которого являются: случайная величина, вероятность, закон распределения случайной величины. Случайной величиной называют числовую функцию от события, могущего носить как количественный (например, инфляция в году T составила х%), так и качественный (например, футбольная команда Manchester United сыграла в Euro-2000 плохо) характер. В первом случае функция от элементарного события – это само событие, а во втором случае эту функцию можно определить как, например, вектор разностей мячей, забитых командой и противниками в соответствующих играх, или гонорары игроков. Вероятность – это числовая функция, определенная на множестве событий. Закон распределения случайной величины ставит в соответствие каждому ее возможному значению определенную вероятность наступления. Уже из определений этих категорий следует набор необходимых условий для моделирования неопределенности в контексте анализа и управления устойчивостью: Вероятности можно задать с помощью закона распределения или определить «вручную» для каждого возможного значения (диапазона значений) случайной величины. В первом случае неопределенность именно моделируется в соответствии с неким математически заданным принципом, а во втором указывается напрямую, исходя из субъективных оценок. Если все вышеуказанные условия выполняются и считается возможным определить вероятность на множестве событий, то моделирование неопределенности можно осуществить. Субъективизм, допущенный при принятии данных условий, являющийся неизбежным свойством любой модели, отражает представления исследователя о поведении управляемой системы в контексте неопределенности, и, следовательно, является одним из необходимых средств познания. События могут быть элементарными и составными. Элементарным событием назовем событие, не могущее быть логически представимо в виде композиции других событий, или такое представление не представляется возможным или целесообразным с точки зрения конкретной задачи. Таким образом, значение или интервал значений исследуемого показателя как случайная величина является функцией от элементарного события. Составное событие, напротив, всегда представимо в виде композиции элементарных событий. Так как событие, заключающееся в том, что управляемая система достигла поставленной цели, является по определению составным (т.к. зависит от значений всех значимых ее параметров), то его вероятность есть некоторая функция от вероятностей тех значений ее параметров, которые удовлетворяют определенным ограничениям на возможность достижения цели. Поэтому и устойчивость относительно поставленной цели рассчитывается как функция от вероятностей тех множеств элементарных событий, при которых поставленная цель достигается, по закону, математически отображающему принцип функционирования управляемой системы. Наиболее предпочтительным способом задания вероятности на множестве элементарных событий является аналитический, т.е. задание закона распределения случайной величины. Его достоинством является абсолютная формализация и упорядоченность вероятностей определенных значений случайной величины в зависимости от двух основополагающих факторов, учитываемых при моделировании неопределенности: рассеяния возможных значений случайной величины от ее ожидаемого значения и удаления определенного значения случайной величины от ожидаемого значения. Кроме того, при выборе конкретной формы кривой распределения, при наличии результатов прогнозирования значений определенного параметра управляемой системы в будущих периодах или состоятельных экспертных оценок, представление его в виде случайной величины является единственным, что повышает объективность метода анализа устойчивости в целом. При задании вероятности аналитическим способом решающим является выбор закона распределения случайной величины. На выбор закона распределения в наиболее значимой степени влияют следующие факторы: С помощью известных статистических выводов и практических навыков, полученных при решении конкретных задач в области инженерной экономики и управления проектами, была составлена следующая Т а б л и ц а 3.1 рекомендуемых вариантов выбора закона распределения случайной величины в зависимости от вышеуказанных факторов. Отметим, что определение показателей закона распределения происходит исходя из данных, полученных в ходе прогнозирования значений анализируемого показателя в будущих периодах и построения доверительного интервала прогноза. Отметим также, что для случаев, в которых информация о влиянии факторов на вариацию исследуемого показателя отсутствует полностью, следует использовать равномерное распределение вида Отметим, что предложенные виды законов распределения далеко не полностью исчерпывают все возможные их виды. Для решения конкретной задачи могут быть использованы особые, проблемно ориентированные формы представления неопределенности. Мощным подспорьем являются также эмпирические данные о «поведении» исследуемого показателя, для обработки которых может быть применим аппарат кривых Пирсона [22, c. 63-70; 21, c. 129-137], получивший солидное теоретическое обоснование в трудах отечественных и зарубежных специалистов в области теории вероятностей. Общая идея метода кривых Пирсона заключается в построении кривой распределения, форма и область определения которой зависят от имеющихся данных о распределении случайной величины (выборки). То есть можно подогнать закон распределения, наиболее адекватно описывающий случайный характер исследуемого показателя, наблюдаемый в ходе статистических исследований, опытов, экспериментов. При подгонке закона распределения под конкретные данные принимается, что полученная выборка является репрезентативной, т.е. адекватно представляет характер вариаций исследуемой случайной величины. Т а б л и ц а 3.1 Варианты выбора закона распределения в зависимости от сочетания влияющих факторов
Пояснения: 1. Биномиальное распределение имеет следующую функцию плотности:
где xmin, xmax – соответственно, нижняя и верхняя границы области определения исследуемого показателя, 2. Распределение Пуассона имеет функцию плотности вида:
Хотя область определения случайной величины, распределенной по закону Пуассона, ограничена только с одной стороны, в практических случаях участком [xmax;¥) можно пренебречь или использовать усеченное распределение Пуассона. 3. Гамма-распределение имеет функцию плотности распределение следующего вида:
где l и r – параметры распределения. Подгонка гамма-распределения к интервалу возможных значений исследуемого показателя, [xmin;xmax], осуществляется путем следующих преобразований:
где xi – определенное значение исследуемого показателя,
где [xinf;xsup] – границы доверительного интервала прогноза, полученные с вероятностью g. Хотя область определения случайной величины, распределенной по гамма-закону, ограничена только с одной стороны, в практических случаях участком [xmax;¥] можно пренебречь или использовать усеченное гамма-распределение. 4. Бета-распределение имеет функцию плотности следующего вида:
где a,b – натуральные числа, большие 1, – параметры бета-распределения, Г(*) – гамма-функция (протабулирована в специальных таблицах). Параметры a,b можно определить, решив систему уравнений:
5. Нормальное (гауссово) распределение имеет следующую функцию плотности:
где s – среднеквадратическое отклонение исследуемого показателя, которое определяется из уравнения (3.5). 6. Логарифмически нормальное распределение имеет неотрицательная случайная величина, логарифм которой имеет нормальное распределение. Функция плотности логарифмически нормального распределения имеет вид:
где s – среднеквадратическое отклонение исследуемого показателя, которое определяется так же, как и в предыдущем случае. 7. Распределение Грама-Шарлье учитывает асимметрию и положительный эксцесс нормального распределения, значения которых выходят за допустимые пределы. Его функция распределения имеет вид [22, c.62]:
8. Функции плотности дискретизированных распределений (бета-, гамма-, нормального, логарифмически нормального, распределения Грама-Шарлье и других возможных непрерывных распределений) имеют общий вид:
где f(x) – соответствующий непрерывный аналог, Dх – шаг дискретизации (расстояние между двумя соседними элементами интервального ряда исследуемого показателя). Метод кривых Пирсона основывается на утверждении, что функции плотности всякого непрерывного распределения,f(x), соответствует дифференциальное уравнение:
где М – мода распределения. Коэффициенты b0,1,2 определяются из системы уравнений:
где
а центральные моменты, mn, оцениваются по выборке с использованием широко известных в статистике формул. Общий интеграл уравнения (3.12) имеет вид:
Конкретный вид интеграла (3.15) зависит от вида корней трехчлена b0x2+b1x+b2. Имеют место три практически значимых случая: Случай 1. Трехчлен имеет вещественные корни различных знаков. Этому случаю соответствует кривая Пирсона следующего вида:
Кривая определена в границах
Случай 2. Трехчлен имеет комплексные корни. Этому случаю соответствует кривая Пирсона следующего вида:
Кривая является асимметричной и определенной для всех вещественных х. Параметры кривой определяются из уравнений:
Случай 3. Трехчлен имеет вещественные корни одного знака. Этому случаю соответствует кривая Пирсона следующего вида:
Кривая простирается от а до ¥, если m3>0, и от -¥ до а, в противном случае. Параметры кривой определяются из уравнений:
Более удобным для практического применения видоизменением Случая 3 является закон распределения вида:
область определения данной функции простирается от а до ¥. Параметры распределения (3.22) оцениваются по имеющейся выборке и рассчитываются путем решения следующей системы уравнений:
где С помощью применения аппарата кривых Пирсона можно получить любое возможное распределение, включаю и те, которые были отмечены в Т а б л и ц е 3.1. Итак, приведенные выше три случая описывают все возможные варианты области определения исследуемого показателя (ограниченная, полуограниченная, неограниченная). Эти непрерывные законы распределения могут быть легко дискретизированы по формуле (3.11). Таким образом, аппарат кривых Пирсона может быть эффективно использован при задании законов распределения исследуемых показателей, какую бы физическую и экономическую природу они не имели. А можно ли применять аппарат кривых Пирсона в случае если статистика исследуемого показателя отсутствует или представлена недостаточным для корректного расчета моментов распределения количеством наблюдений? Можно, если принять следующие допущения: 1. Ожидаемое значение исследуемого показателя является точкой максимума функции плотности его распределения, т.е. для любого сколь угодно малого e выполняется:
где D – область определения исследуемого показателя. При 2. Справедливо равенство (3.5). 3. Параметры кривой распределения однозначно определяются ее видом (f(x)), условием (3.22) и равенством (3.5). Эти предположения справедливы в большинстве практических случаев. В самом деле, ожидаемое значение – это, как правило, наиболее вероятное значение исследуемого показателя; в противном случае, прогноз нелогичен. Верность допущения 2 вытекает из самого определения надежности доверительного интервала прогноза как вероятности попадания фактического значения исследуемого показателя в построенный для него доверительный интервал. Верность допущения 3 доказывается от противного: можно показать, что альтернативная комбинация параметров кривой, удовлетворяющая любым двум условиям, не удовлетворяет третьему условию; а альтернативная комбинация, удовлетворяющая всем трем условиям, совпадает с исходной комбинацией, что доказывает единственность исходной комбинации параметров кривой. При условии верности вышеуказанных допущений, значения параметров кривых для трех рассматриваемых случаев приведены ниже. Случай 1. Параметры кривой находятся из уравнений:
Случай 2. Параметры кривой находятся из уравнений:
Случай 3. Параметры кривой находятся из уравнений:
Итак, получили, что при допущениях весьма общего характера можно моделировать неопределенность исследуемых показателей во всех практически значимых случаях. При этом моделью выступает закон распределения случайной величины, соответствующей исследуемому показателю. * Данное допущение выполняется автоматически при задании для случайной величины алгебраически представимого закона распределения. Интересующихся математической стороной вопроса отсылаем к известной в теории меры теореме Каратеодори, утверждающей возможность однозначного определения вероятности любого события, входящего в алгебру событий, на которой определена вероятность. (См., напр., [24, с. 172]). * «Усеченное» означает определенное только в области определения исследуемого показателя. В ряде случаев полезно вводить поправку на усеченность распределения: f*(x) = f(x)/[F(b)-F(a)], где f*(x) – функция распределения с учетом поправки исходной функции распределения f(x) на усеченность, F(a), F(b) – значения интегральной функции распределения на концах области определения исследуемого показателя ([18, c. 273-274]). |
||||||||||||||||
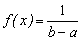 , где a,b – соответственно, нижняя и верхняя границы области определения исследуемого показателя.
, где a,b – соответственно, нижняя и верхняя границы области определения исследуемого показателя.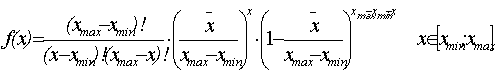 (3.1)
(3.1)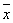 – его ожидаемое значение.
– его ожидаемое значение.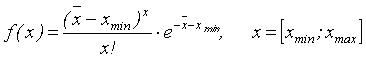 (3.2)
(3.2)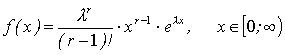 (3.3)
(3.3)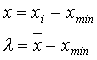 (3.4)
(3.4)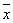 – его ожидаемое значение. Значение параметра r можно найти из уравнения:
– его ожидаемое значение. Значение параметра r можно найти из уравнения: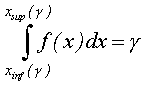 (3.5)
(3.5)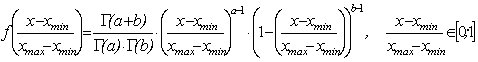 (3.6)
(3.6)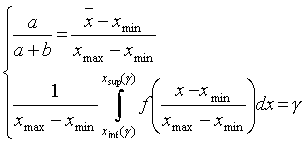 (3.7)
(3.7)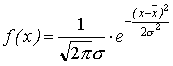 (3.8)
(3.8)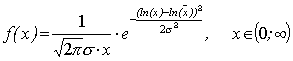 (3.9)
(3.9)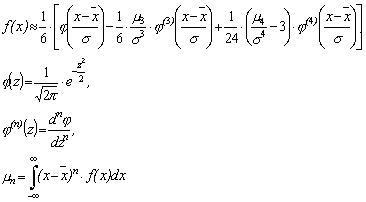 (3.10)
(3.10)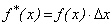 (3.11)
(3.11)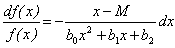 (3.12)
(3.12)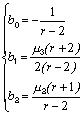 (3.13)
(3.13)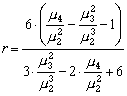 (3.14)
(3.14)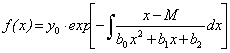 (3.15)
(3.15)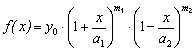 (3.16)
(3.16)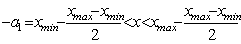 . Остальные параметры кривой определяются из следующих уравнений:
. Остальные параметры кривой определяются из следующих уравнений: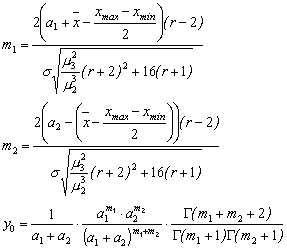 (3.17)
(3.17)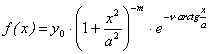 (3.18)
(3.18)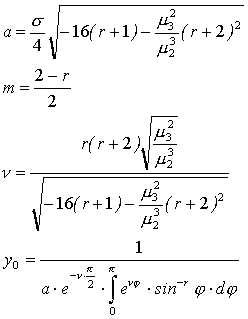 (3.19)
(3.19)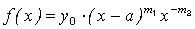 (3.20)
(3.20)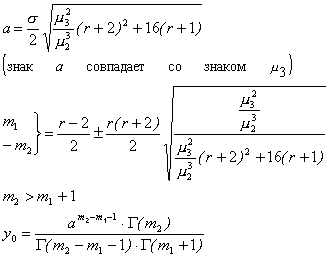 (3.21)
(3.21)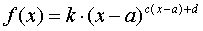 (3.22)
(3.22)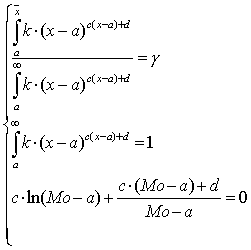 (3.23)
(3.23)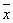 – среднее значение выборки, Мо – мода выборочного распределения (наиболее часто встречающееся значение),g – соотношение числа наблюдений, меньших или равных среднего значения, к объему выборки.
– среднее значение выборки, Мо – мода выборочного распределения (наиболее часто встречающееся значение),g – соотношение числа наблюдений, меньших или равных среднего значения, к объему выборки.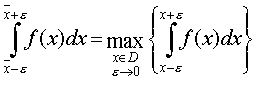 (3.24)
(3.24)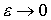
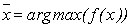 .
.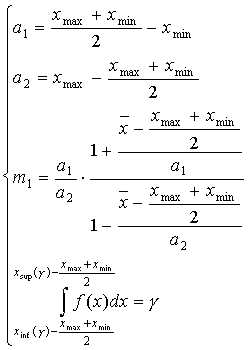 (3.25)
(3.25)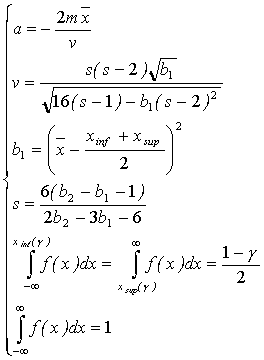 (3.26)
(3.26)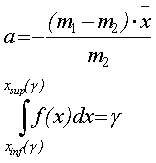 (3.27)
(3.27)