«Управление и Оптимизация Производственного Предприятия»
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
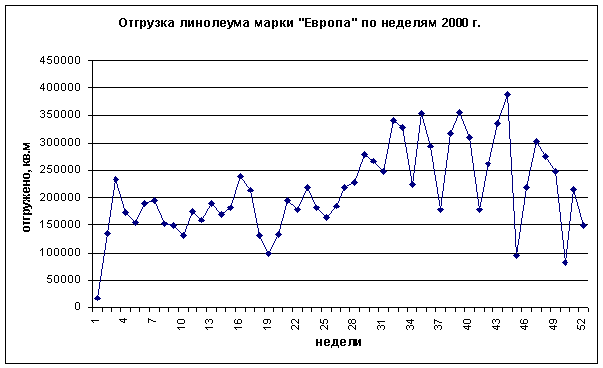
Анализ устойчивости относительно поставленной цели как один из подходов к описанию функционирования организации в условиях неопределенности Монография, Самара, 2001. Глава 7. Возможности практической реализации методики анализа и управления устойчивостью относительно поставленной цели на примере ОАО «Синтерос» (г. Отрадный) В данной главе содержатся результаты методической работы, проведенной с использованием материалов, предоставленных ОАО «Синтерос» и кафедрой «Экономика промышленности» СамГТУ для выяснения возможностей использования предлагаемой методики и сравнения полученных с ее помощью результатов с результатами, полученными путем применения традиционной методики. Объектом исследования была проблема расчета плановых заданий на производство продукции в условиях неопределенности спроса. Предварительные замечания ОАО «Синтерос» – одно из ведущих промышленных предприятий г. Отрадный, занимающееся производством линолеума и топлинга 7 видов. По результатам 2000 г. было отгружено чуть более 16,209 млн. кв. м продукции. Наиболее ходовыми товарами ОАО «Синтерос» являются линолеум марки «Европа», которого было отгружено 11,030 млн. кв. м, или 68,05% от общей величины отгруженной продукции, и линолеум марки «Конкурент», которого было отгружено 4,968 млн. кв. м, или 30,65% от общей величины отгруженной продукции. Динамика отгрузки этих марок линолеумов представлена на р и с. 7.1 и р и с. 7.2.
Р и с. 7.1. Динамика отгрузки линолеума марки «Европа». Как видно из представленных графиков, объемы отгрузки ведущих марок линолеума, производимых ОАО «Синтерос», сильно варьируют в зависимости от периода, причем колебания объемов отгрузки усиливаются к концу 2000 г. Это связано с тем, что предприятие работает по прямым заказам, которые поступают неравномерно. В связи с этим возникает проблема более адекватного спросу планирования производства.
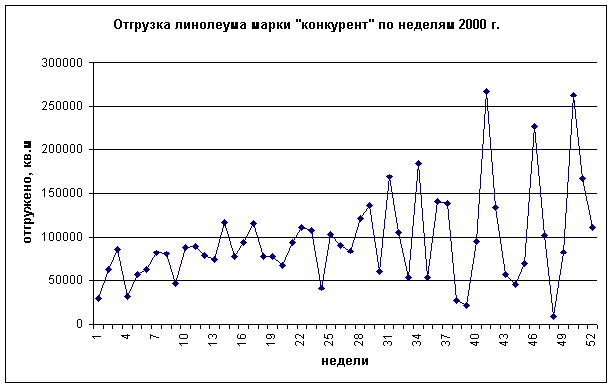
Р и с. 7.2. Динамика отгрузки линолеума марки «Конкурент». В современных экономических условиях величина спроса на продукцию в течение периода планирования редко может быть предсказана с приемлемой точностью, в то время как плановые показатели объемов производства продукции должны быть определены в начале периода планирования. Несоответствие производимых объемов продукции запрашиваемым вызывает финансовые и экономические потери, вызванные следующими причинами: а) В случае преобладания объемов произведенной продукции над величиной спроса на нее возникает необходимость хранения и (или) утилизации излишков, что, наряду с затратами на хранение и утилизацию, может вызвать издержки, связанные с естественной убылью продукции, потерей товарного вида, а также замораживанием оборотных средств в недостаточно ликвидных активах. б) В случае преобладания величины спроса над имеющимся количеством продукции возникают потери, обусловленные упущенной прибылью от реализации недостающего количества продукции, потерей клиентов и деловой репутации фирмы. Существование потерь, вызванных несоответствием величины спроса на продукцию и имеющимся ее количеством, ставит задачу оптимизации объемов плановых заданий по производству продукции. Причем при расчете оптимальных плановых заданий необходимо учитывать фактор неопределенности спроса как основной. Учет фактора неопределенности обычно производится путем представления спроса на продукцию в виде случайной величины. Случайной величиной в статистике называют величину, могущую принимать различные значения от опыта к опыту. Случайные величины бывают непрерывные и дискретные. Непрерывные случайные величины могут принимать практически несчетное количество значений (например, рост человека является непрерывной случайной величиной). Дискретные случайные величины могут принимать счетное количество значений (например, число бракованных деталей в партии является дискретной случайной величиной), однако при достаточно большом числе значений, которые может принимать дискретная случайная величина, ее можно приближенно считать непрерывной. Поведение случайной величины принято описывать законом распределения ее вероятностей – математической функцией, задающей для каждого возможного значения дискретной случайной величины или для интервала значений непрерывной случайной величины вероятность его реализации. Большая часть встречающихся на практике случайных величин (к которой относится и величина спроса на продукцию) имеют следующие базовые характеристики: а) математическое ожидание, равное сумме произведений всех возможных значений случайной величины на вероятности их появления:
где Хi – множество значений, которые может принимать случайная величина Х, р(Хi) – вероятности реализаций соответствующих значений. Для непрерывных случайных величин формула математического ожидания имеет вид:
где f(x) – функция плотности распределения вероятностей непрерывной случайной величины Х, xinf,sup – соответственно, нижняя и верхняя границы области возможных значений случайной величины Х. б) среднеквадратическое, или стандартное отклонение:
для дискретных случайных величин и
На практике математическое ожидание и стандартное отклонение оценивают по выборке – доступному для исследования множеству реализаций случайной величины (например, объем продаж за годичный период). Так, по имеющейся выборке, математическое ожидание спроса на линолеум марок «Европа» и «Конкурент» составляет, соответственно, 212120,1 и 95552,96 кв. м в неделю, а стандартное отклонение – соответственно, 77958,71 и 54402,87 кв. м в неделю. Общий подход к решению задачи оптимизации планового задания в условиях неопределенности спроса заключается в минимизации выбранного критерия, который, как правило, является функцией от объема планового задания и параметров закона распределения спроса. Вид критерия разрабатывается в процессе постановки задачи для конкретного случая. Общая постановка задачи Так как объемы отгрузки линолеума выражаются в десятках тысяч кв. м в неделю, величину спроса на линолеум можно считать непрерывной случайной величиной. Пусть производится n видов продукции в количествах Задачу оптимизации планового задания можно поставить относительно трех различных видов критериев: 1. Критерий минимума математического ожидания потерь от несовпадения имеющегося количества продукции с величиной спроса на нее при стационарном спросе (т.е. в наблюдаемой динамике спроса отсутствует тенденция: величина спроса колеблется около некоторого среднего уровня). В данном случае задача решается методом маргинального анализа. Предположим, что плановое задание составляет vi – 1 единиц. При увеличении планового задания на 1 единицу издержки, связанные с нехваткой единицы продукции, сокращаются на c2i с вероятностью
Понятно, что производство следует наращивать до тех пор, пока DМ ³ 0. Из условия DМ ³ 0 получаем, что оптимальное значение производственного задания, v*i, находится из уравнения, предложенного в [17, c. 19]:
Учитывая допущение о непрерывности случайной величины спроса, путем предельного перехода уравнение (7.6) легко преобразуется в уравнение:
2. Критерий минимума математического ожидания потерь от несовпадения имеющегося количества продукции с величиной спроса на нее при нестационарном спросе (т.е. в наблюдаемой динамике спроса присутствует тенденция). Использование данного критерия также приводит к уравнению (7.7), однако логика, применяемая здесь, другая. Математическое ожидание потерь от несовпадения имеющегося количества продукции вида i с величиной спроса на нее можно выразить по формуле:
Для минимизации функции (7.8), возьмем производную по vi и приравняем ее к нулю, откуда получаем, что оптимальный, с точки зрения критерия минимума математического ожидания потерь от несовпадения имеющегося количества продукции с величиной спроса на нее, объем планового задания, v*i находится путем решения уравнения (7.7). Другим отличием данного критерия является то, что при наличии тенденции в динамике спроса, параметры функции плотности распределения его вероятностей меняются в каждом последующем периоде планирования. 3. Критерий максимума вероятности достижения уровня потерь от несовпадения планового задания с величиной спроса, меньшего или равного некоторого заданного значения Ai (или критерий максимума устойчивости относительно поставленной цели):
Данный критерий в своем применении опирается не на математическое ожидание потерь, а на их реальное значение – это является его преимуществом над критериями (7.5) и (7.6), – и его логика заключается в следующем:
Учитывая (7.12), по формуле полной вероятности, получаем:
Дифференцируя (7.13) по vi, получаем, что оптимальное значение производственного задания, v*i, находится из уравнения:
Далее мы сравним результаты решения задачи по предложенным критериям и разработаем рекомендации по определению плановых заданий на первые 12 недель 2001 г. Статистический анализ корреляционной связи и прогнозирование будущих значений рядов динамики отгрузки продукции Получение решения по критерию (7.5) предполагает стационарность спроса на продукцию, т.е. отсутствие тенденции в динамике данной величины. Тенденция в статистическом анализе характеризуется существованием линейного тренда как одной из компонент анализируемого временного ряда (выборки, упорядоченной по времени наблюдений), наряду с сезонной (проявляющейся в циклических колебаниях значений ряда) и случайной (проявляющейся в виде бессистемных, случайных отклонений остатков значений временного ряда после вычета из них тренда и сезонной компоненты от нулевого уровня) компонентами. Простым, но надежным способом проверки наличия линейного тренда является расчет коэффициента корреляции между наблюдениями и соответствующими им временными аргументами (в данном случае, номерами недель) и проверка его на статистическую значимость. Коэффициент корреляции показывает существование линейной связи между наблюдениями и временными аргументами: чем ближе он к 1 или –1, тем эта связь более тесна. В случае если найденный коэффициент корреляции окажется статистически значимым, применять критерий (7.5) некорректно. Для оценки коэффициента корреляции между наблюдениями и соответствующими им временными аргументами в статистике используется следующая формула:
где Xi – наблюдения (в данном случае – величины отгрузки), ti – номера недель, n – количество наблюдений. Коэффициент корреляции также является случайной величиной, т.к. его численное значение зависит от значений наблюдений выборки. Проверка коэффициента корреляции на статистическую значимость проводится с целью выяснить, не равно ли его математическое ожидание нулю, т.е. действительно ли существует искомая линейная связь. Эта проверка осуществляется путем сравнения величины Исходные данные для статистического анализа приведены в Т а б л и ц а х 7.1, 7.2. Для линолеума марки «Европа» коэффициент корреляции составил 0,47, а для «Конкурента» 0,367. При уровне значимости 0,05 корреляционная взаимосвязь в обоих случаях оказывается статистически значимой. Поэтому применение критерия (7.5) в нашем случае некорректно. Для применения оставшихся двух критериев необходимо получить прогнозы отгрузки «Европы» и «Конкурента» и рассчитать их доверительные интервалы. Затем следует определить вид закона распределения отклонений расчетных значений, полученных путем наложения математической модели динамики, используемой при получении прогноза, на фактические данные, от наблюдаемых значений исследуемых показателей. Затем, имея доверительные интервалы прогноза, построенные для каждого периода прогнозирования, и вид закона распределения остатков, можно определить параметры закона распределения будущих значений исследуемых показателей для каждого периода прогнозирования. Т а б л и ц а 7.1 Отгрузка линолеума марки «Европа» по неделям 2000 г.
Т а б л и ц а 7.2 Отгрузка линолеума марки «Конкурент» по неделям 2000 г.
Прогнозы будущих значений величин отгрузки для линолеумов «Европа» и «Конкурент», а также их доверительные интервалы с надежностью 0,9,* полученные с помощью программы «СтатЭксперт», приведены в Т а б л и ц а х 7.3, 7.4. Т а б л и ц а 7.3 Прогноз отгрузки линолеума марки «Европа» на первые 12 недель 2001 г.
Т а б л и ц а 7.4 Прогноз отгрузки линолеума марки «Конкурент» на первые 12 недель 2001 г.
Отклонения расчетных от фактически наблюдаемых значений отгрузки линолеумов «Европа» и «Конкурент» приведены в Т а б л и ц а х 7.5, 7.6. Т а б л и ц а 7.5 Отклонения расчетных от фактически наблюдаемых значений отгрузки линолеума «Европа»
Среднее значение – 1352,8 кв. м в неделю Стандартное отклонение – 20707 кв. м в неделю Т а б л и ц а 7.6 Отклонения расчетных от фактически наблюдаемых значений отгрузки линолеума «Конкурент»
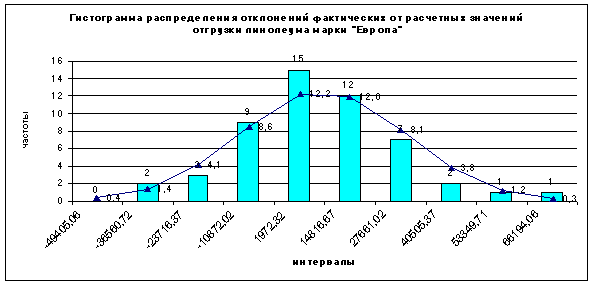
Среднее значение – -761,1 кв. м в неделю Стандартное отклонение – 37308 кв. м в неделю Для выяснения вида закона распределения отклонений построим гистограммы этих отклонений. Гистограммой в статистике называют особый вид графика, по горизонтальной оси которого идут интервалы, на которые был разбит диапазон изменения исследуемого показателя, а по вертикальной – частоты (количества попаданий в соответствующие интервалы). По виду гистограммы выдвигается гипотеза о соответствии закона распределения исследуемого показателя предполагаемому. Гистограммы распределения отклонений расчетных от фактических значений отгрузки для линолеумов «Конкурент» и «Европа» приведены на Р и с. 7.3, 7.4.
Р и с. 7.3.
Р и с. 7.4. Непрерывной линией показан частоты, которые наблюдались бы нормальном законе распределения отклонений, имеющем вид:
Для проверки гипотезы о соответствии фактического закона распределения предполагаемому применяется критерий Пирсона:
где k – число точек сравнения (в нашем случае – число интервалов разбиения), Оk – наблюдаемая частота, Еk – ожидаемая частота. Величина (7.17) подчиняется «хи-квадрат» распределению с к-1-p степенями свободы, где р – число параметров предполагаемого закона распределения (в нашем случае р=2). Если рассчитанная величина (7.17) окажется больше табличной при выбранном уровне значимости, то нельзя считать, что фактическое распределение соответствует предполагаемому. Для применения критерия интервалы объединяют таким образом, чтобы в каждом интервале наблюдаемая частота была не меньше 5. Выберем уровень значимости 0,25. Наблюдаемое значение критерия для «Европы» – 1,167, для «Конкурента» – 0,482; критическое же значение при уровне значимости 0,25 – 1,213. Таким образом, отклонения и в одном, и в другом случаях можно считать имеющими нормальное распределение. Так как отклонения являются случайными по своей природе и получены путем наложения аппроксимационной модели на фактические данные, можно считать, что их математические ожидания равны нулю. Тогда математические ожидания будущих значений показателей отгрузки для каждого i-го периода прогноза можно считать равными точечным значениям прогноза. Стандартные отклонения будущих значений показателей отгрузки для каждого i-го периода прогноза получаются из уравнения:
Результаты расчетов приведены в Т а б л и ц е 7.7.
Т а б л и ц а 7.7 Стандартные отклонения прогнозов отгрузки для каждого периода прогнозирования
Результаты решения задачи Пусть затраты, вызванные излишком линолеума марок «Европа» и «Конкурент», составляют 1,5 руб. с каждого кв. м, а затраты, связанные с нехваткой, – соответственно, 7,5 и 7 руб. с каждого кв. м. Применение критериев (7.8) и (7.9) (соответственно, минимум математического ожидания потерь от несовпадения величины спроса и планового задания и максимум вероятности достижения уровня потерь, меньшего или равного заданному) дают результаты, превосходящие соответствующие прогнозные значения, что вызвано необходимостью создания некоторого «страхового запаса» на случай неожиданного превышения фактического спроса над ожидаемым. В Т а б л и ц а х 7.8, 7.9 приведены результаты применения критериев (7.8) и (7.9). Как можно увидеть из этих таблиц, превышение рекомендуемых плановых заданий над прогнозами во всех случаях довольно существенно, однако в случае применения критерия (7.9) оно меньше, чем в случае применения критерия (7.8). Это говорит о том, что критерий (7.8) предполагает больший «страховой запас», чем критерий (7.9). С одной стороны, больший «страховой запас» означает большую уверенность в том, что все поступившие заказы будут удовлетворены; но, с другой стороны, это означает менее рациональное использование оборотных средств, опасность затоваривания и потери ритмичности производства, учитывая, что в данном случае остатки предыдущей недели переходят полностью в запасы на текущей неделе (нет естественной убыли). Т а б л и ц а 7.8 Рекомендованные по критерию (7.8) плановые задания в сравнении с прогнозами отгрузки на первые 12 недель 2001 г. (в кв. м)
Т а б л и ц а 7.9 Рекомендованные по критерию (7.9) плановые задания в сравнении с прогнозами отгрузки на первые 12 недель 2001 г. (в кв. м)*
Какой же из двух предлагаемых вариантов плановых заданий выбрать? Или, может быть, следует выбрать некоторую комбинацию вариантов? При выборе необходимо учитывать следующие факторы:
Сопоставление рекомендуемых плановых заданий и вторичных характеристик– ожидаемых потерь и вероятностей достижения заданного уровня потерь – по двум вариантам приведено в Т а б л и ц а х 7.10, 7.11. Т а б л и ц а 7.10 Сопоставление рекомендуемых плановых заданий
Как видно из Т а б л и ц ы 7.10, результаты решения задачи по критериям (7.8) и (7.9) отличаются друг от друга весьма незначительно относительно рассчитанных их значений (различие всегда менее 10% от абсолютных величин). Однако более глубокий анализ результатов позволяет выявить более существенные различия между ними, о чем говорят данные Т а б л и ц ы 7.11. Т а б л и ц а 7.11 Сопоставление вторичных характеристик вариантов
Как видно из проведенного сопоставления, разница между рекомендуемыми плановыми заданиями и вторичными характеристиками двух сравниваемых вариантов невелика. Однако учитывая факторы, влияющие на выбор варианта, можно предложить комбинацию двух вариантов плановых заданий, состоящую в следующем:
Наглядно рекомендуемые плановые задания представлены в Т а б л и ц е 7.12.
Т а б л и ц а 7.12 Рекомендуемые значения плановых заданий
Практические аспекты реализации полученных результатов Данная работа носила в основном методический характер, поэтому расчеты произведены не на текущий, а на произвольно выбранный момент. Ее результаты позволяют сделать следующие два замечания по поводу практической реализации методики:
Приведенные меры позволят минимизировать затраты времени и усилий на расчеты плановых заданий и одновременно контролировать движение товара с достаточной для практических целей дискретностью.
* Доверительным интервалом прогноза с заданной надежностью называется интервал, в котором окажется фактическое значение прогнозируемого показателя с вероятностью, равной заданному значению надежности. Ширина доверительного интервала прямо зависит от ошибки аппроксимации фактических данных и обратно – от числа наблюдений. * При использовании критерия (7.9) задаваемое значение потерь составляло 100 тыс. руб. в неделю. * Имеется в виду среднее хронологическое значение вероятности. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
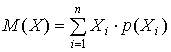 (7.1)
(7.1)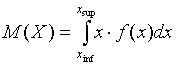 (7.2)
(7.2)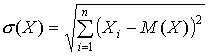 (7.3)
(7.3)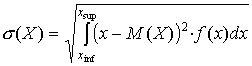 (7.4)
(7.4)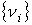 единиц,i=1…n. Обозначим величину спроса на продукцию вида i через yi, потери, связанные с излишком единицы продукции вида i через c1i, потери, связанные с нехваткой единицы продукции вида i через c2i, и функцию плотности распределения вероятностей спроса на продукцию вида i через fi(yi).
единиц,i=1…n. Обозначим величину спроса на продукцию вида i через yi, потери, связанные с излишком единицы продукции вида i через c1i, потери, связанные с нехваткой единицы продукции вида i через c2i, и функцию плотности распределения вероятностей спроса на продукцию вида i через fi(yi).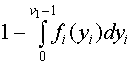 , но издержки, связанные с излишком единицы продукции, возрастают на c1i с вероятностью
, но издержки, связанные с излишком единицы продукции, возрастают на c1i с вероятностью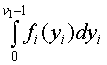 ; итого получаем, что прирост математического ожидания дохода от производства дополнительной единицы продукции составит
; итого получаем, что прирост математического ожидания дохода от производства дополнительной единицы продукции составит (7.5)
(7.5)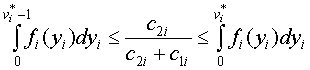 (7.6)
(7.6)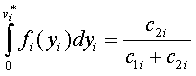 (7.7)
(7.7) (7.8)
(7.8)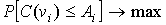 (7.9)
(7.9)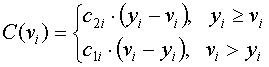 (7.10)
(7.10)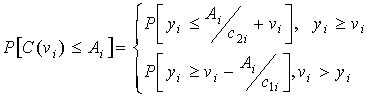 (7.11)
(7.11)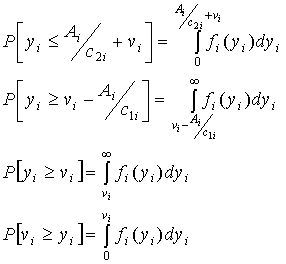 (7.12)
(7.12)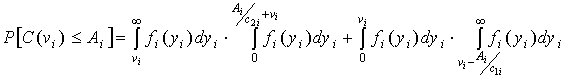 (7.13)
(7.13)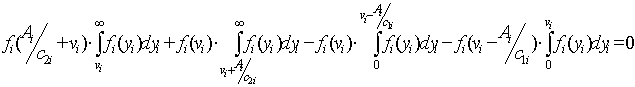 (7.14)
(7.14)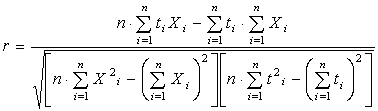 (7.15)
(7.15)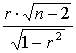 с критическим значением распределения Стьюдента, t(n-2,1-a), при n-2 степенях свободы и уровне значимости a (берется из статистических таблиц). Уровень значимости показывает вероятность ошибки счесть рассчитанный коэффициент корреляции статистически значимым, в то время как он на самом деле не является таковым. Обычно уровень значимости берется равным 0,05.
с критическим значением распределения Стьюдента, t(n-2,1-a), при n-2 степенях свободы и уровне значимости a (берется из статистических таблиц). Уровень значимости показывает вероятность ошибки счесть рассчитанный коэффициент корреляции статистически значимым, в то время как он на самом деле не является таковым. Обычно уровень значимости берется равным 0,05.
 (7.16)
(7.16)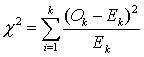 (7.17)
(7.17)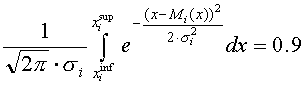 (7.18)
(7.18)