«Управление и Оптимизация Производственного Предприятия»
|
|
|
||||||||||||||||||||||
|
Теория принятия решений Учебное пособие. - М.: Издательство "Март", 2004. 2. ОПИСАНИЕ НЕОПРЕДЕЛЕННОСТЕЙ В ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ 2.2. Вероятностно-статистические методы описания неопределенностей в теории принятия решений 2.2.2. Основы теории вероятностейЭтот раздел содержит полные доказательства всех рассматриваемых утверждений. События и вероятности. Исходное понятие при построении вероятностных моделей в задачах принятия решений – опыт (испытание). Примерами опытов являются проверка качества единицы продукции, бросание трех монет независимо друг от друга и т.д. Первый шаг при построении вероятностной модели реального явления или процесса – выделение возможных исходов опыта. Их называют элементарными событиями. Обычно считают, что в первом опыте возможны два исхода – «единица продукции годная» и «единица продукции дефектная». Естественно принять, что при бросании монеты осуществляется одно из двух элементарных событий – «выпала решетка (цифра)» и «выпал герб». Таким образом, случаи «монета встала на ребро» или «монету не удалось найти» считаем невозможными. При бросании трех монет элементарных событий значительно больше. Вот одно из них – «первая монета выпала гербом, вторая – решеткой, третья – снова гербом». Перечислим все элементарные события в этом опыте. Для этого обозначим выпадение герба буквой Г, а решетки – буквой Р. Имеется 23=8 элементарных событий: ГГГ, ГГР, ГРГ, ГРР, РГГ, РГР, РРГ, РРР – в каждой тройке символов первый показывает результат бросания первой модели, второй – второй монеты, третий – третьей монеты. Совокупность всех возможных исходов опыта, т.е. всех элементарных событий, называется пространством элементарных событий. Вначале мы ограничимся пространством элементарных событий, состоящим из конечного числа элементов. С математической точки зрения пространство (совокупность) всех элементарных событий, возможных в опыте – это некоторое множество, а элементарные события – его элементы. Однако в теории вероятностей для обозначения используемых понятий по традиции используются свои термины, отличающиеся от терминов теории множеств. В табл. 1 установлено соответствие между терминологическими рядами этих двух математических дисциплин. Таблица 1. Соответствие терминов теории вероятностей и теории множеств
Как сложились два параллельных терминологических ряда? Основные понятия теории вероятностей и ее терминология сформировались в XVII-XVIII вв. Теория множеств возникла в конце XIX в. независимо от теории вероятностей и получила распространение в ХХ в. Принятый в настоящее время аксиоматический подход к теории вероятностей, разработанный академиком АН СССР А.Н. Колмогоровым (1903-1987), дал возможность развивать эту дисциплину на базе теории множеств и теории меры. Этот подход позволил рассматривать теорию вероятностей и математическую статистику как часть математики, проводить рассуждения на математическом уровне строгости. В частности, было введено четкое различие между частотой и вероятностью, случайная величина стала рассматриваться как функция от элементарного исхода, и т.д. За основу методов статистического анализа данных стало возможным брать вероятностно-статистические модели, сформулированные в математических терминах. В результате удалось четко отделить строгие утверждения от обсуждения философских вопросов случайности, преодолеть подход на основе понятия равновозможности, имеющий ограниченное практическое значение. Наиболее существенно, что после работ А.Н.Колмогорова нет необходимости связывать вероятности тех или иных событий с пределами частот. Так называемые «субъективные вероятности» получили смысл экспертных оценок вероятностей. После выхода (в 1933 г. на немецком языке и в 1936 г. – на русском) основополагающей монографии [4] аксиоматический подход к теории вероятностей стал общепринятым в научных исследованиях в этой области. Во многом перестроилось преподавание. Повысился научный уровень многих прикладных работ. Однако традиционный подход оказался живучим. Распространены устаревшие и во многом неверные представления о теории вероятностей и математической статистике. Поэтому в настоящей главе рассматриваем основные понятия, подходы, идеи, методы и результаты в этих областях, необходимые для их квалифицированного применения в задачах принятия решений. В послевоенные годы А.Н.Колмогоров формализовал понятие случайности на основе теории информации [5]. Грубо говоря, числовая последовательность является случайной, если ее нельзя заметно сжать без потери информации. Однако этот подход не был предназначен для использования в прикладных работах и преподавании. Он представляет собой важное методологическое и теоретическое продвижение. Перейдем к основному понятию теории вероятностей – понятию вероятности события. В методологических терминах можно сказать, что вероятность события является мерой возможности осуществления события. В ряде случаев естественно считать, что вероятность события А – это число, к которому приближается отношение количества осуществлений события А к общему числу всех опытов (т.е. частота осуществления события А) – при увеличении числа опытов, проводящихся независимо друг от друга. Иногда можно предсказать это число из соображений равновозможности. Так, при бросании симметричной монеты и герб, и решетка имеют одинаковые шансы оказаться сверху, а именно, 1 шанс из 2, а потому вероятности выпадения герба и решетки равны 1/2. Однако этих соображений недостаточно для развития теории. Методологическое определение не дает численных значений. Не все вероятности можно оценивать как пределы частот, и неясно, сколько опытов надо брать. На основе идеи равновозможности можно решить ряд задач, но в большинстве практических ситуаций применить ее нельзя. Например, для оценки вероятности дефектности единицы продукции. Поэтому перейдем к определениям в рамках аксиоматического подхода на базе математической модели, предложенной А.Н.Колмогоровым (1933). Определение 1. Пусть конечное множество
Тогда пара
Сконструирован математический объект, основной при построении вероятностных моделей. Рассмотрим примеры. Пример 1. Бросанию монеты соответствует вероятностное пространство с Пример 2. Проверке качества одной единицы продукции (в ситуации, описанной в романе А.Н.Толстого «Хождение по мукам» - см. выше) соответствует вероятностное пространство с Отметим, что определение Р(А) согласуется с интуитивным представлением о связи вероятностей события и входящих в него элементарных событий, а также с распространенным мнением, согласно которому «вероятность события А – число от 0 до1, которое представляет собой предел частоты реализации события А при неограниченном числе повторений одного и того же комплекса условий». Из определения вероятности события, свойств символа суммирования и равенства (1) вытекает, что
При практическом применении вероятностно-статистических методов принятия решений постоянно используется понятие независимости. Например, при применении статистических методов управления качеством продукции говорят о независимых измерениях значений контролируемых параметров у включенных в выборку единиц продукции, о независимости появления дефектов одного вида от появления дефектов другого вида, и т.д. Независимость случайных событий понимается в вероятностных моделях в следующем смысле. Определение 2. События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Это определение соответствует интуитивному представлению о независимости: осуществление или неосуществление одного события не должно влиять на осуществление или неосуществление другого. Утверждение 1. Пусть события А и В независимы. Тогда события Действительно, из свойства в) в (3) следует, что для событий С и D, произведение которых пусто, P(C+D) = P(C) +P(D). Поскольку пересечение АВ и Вывод равенства Р(А Для доказательства независимости Пример 3. Рассмотрим опыт, состоящий в бросании игрального кубика, на гранях которого написаны числа 1, 2, 3, 4, 5,6. Считаем, что все грани имеют одинаковые шансы оказаться наверху. Построим соответствующее вероятностное пространство. Покажем, что события «наверху – грань с четным номером» и «наверху – грань с числом, делящимся на 3» являются независимыми. Разбор примера. Пространство элементарных исходов состоит из 6 элементов: «наверху – грань с 1», «наверху – грань с 2»,…, «наверху – грань с 6». Событие «наверху – грань с четным номером» состоит из трех элементарных событий – когда наверху оказывается 2, 4 или 6. Событие «наверху – грань с числом, делящимся на 3» состоит из двух элементарных событий – когда наверху оказывается 3 или 6. Поскольку все грани имеют одинаковые шансы оказаться наверху, то все элементарные события должны иметь одинаковую вероятность. Поскольку всего имеется 6 элементарных событий, то каждое из них имеет вероятность 1/6. По определению 1событие «наверху – грань с четным номером» имеет вероятность Ѕ, а событие «наверху – грань с числом, делящимся на 3» - вероятность 1/3. Произведение этих событий состоит из одного элементарного события «наверху – грань с 6», а потому имеет вероятность 1/6. Поскольку 1/6 = Ѕ х 1/3, то рассматриваемые события являются независимыми в соответствии с определением независимости. В вероятностных моделях процедур принятия решений с помощью понятия независимости событий можно придать точный смысл понятию «независимые испытания». Для этого рассмотрим сложный опыт, состоящий в проведении двух испытаний. Эти испытания называются независимыми, если любые два события А и В, из которых А определяется по исходу первого испытания, а В – по исходу второго, являются независимыми. Пример 4. Опишем вероятностное пространство, соответствующее бросанию двух монет независимо друг от друга. Разбор примера. Пространство элементарных событий состоит из четырех элементов: ГГ, ГР, РГ, РР (запись ГГ означает, что первая монета выпала гербом и вторая – тоже гербом; запись РГ – первая – решеткой, а вторая – гербом, и т.д.). Поскольку события «первая монета выпала решеткой» и «вторая монета выпала гербом» являются независимыми по определению независимых испытаний и вероятность каждого из них равна Ѕ, то вероятность РГ равна ј. Аналогично вероятность каждого из остальных элементарных событий также равна ј. Пример 5. Опишем вероятностное пространство, соответствующее проверке качества двух единиц продукции независимо друг от друга, если вероятность дефектности равна х. Разбор примера. Пространство элементарных событий состоит из четырех элементов: Вероятность того, что единица продукции дефектна, есть х, а потому вероятность того, что имеет место противоположное событие, т.е. единица продукции годна, есть 1 – х. Поскольку результат проверки первой единицы продукции не зависит от такового для второй, то Случайные величины и их математические ожидания. Случайная величина – это величина, значение которой зависит от случая, т.е. от элементарного события Определение случайной величины Х как функции от элементарного события Отметим, что элементы Н – это не обязательно числа. Ими могут быть и последовательности чисел (вектора), и функции, и математические объекты иной природы, в частности, нечисловой (упорядочения и другие бинарные отношения, множества, нечеткие множества и др.) [2]. Однако наиболее часто рассматриваются вероятностные модели, в которых элементы Н – числа, т.е. Н = R1. В иных случаях обычно используют термины «случайный вектор», «случайное множество», «случайное упорядочение», «случайный элемент» и др. Рассмотрим случайную величину с числовыми значениями. Часто оказывается полезным связать с этой функцией число – ее «среднее значение» или, как говорят, «среднюю величину», «показатель центральной тенденции». По ряду причин, некоторые из которых будут ясны из дальнейшего, в качестве «среднего значения» обычно используют математическое ожидание. Определение 3. Математическим ожиданием случайной величины Х называется число
т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий. Пример 6. Вычислим математическое ожидание числа, выпавшего на верхней грани игрального кубика. Непосредственно из определения 3 следует, что
Утверждение 2. Пусть случайная величина Х принимает значения х1, х2,…, хm. Тогда справедливо равенство
т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям того, что случайная величина принимает определенные значения. В отличие от (4), где суммирование проводится непосредственно по элементарным событиям, случайное событие Иногда соотношение (5) принимают как определение математического ожидания. Однако с помощью определения 3, как показано далее, более легко установить свойства математического ожидания, нужные для построения вероятностных моделей реальных явлений, чем с помощью соотношения (5). Для доказательства соотношения (5) сгруппируем в (4) члены с одинаковыми значениями случайной величины
Поскольку постоянный множитель можно вынести за знак суммы, то
По определению вероятности события
С помощью двух последних соотношений получаем требуемое:
Понятие математического ожидания в вероятностно-статистической теории соответствует понятию центра тяжести в механике. Поместим в точки х1, х2,…, хm на числовой оси массы P(X=x1), P(X=x2),…, P(X=xm) соответственно. Тогда равенство (5) показывает, что центр тяжести этой системы материальных точек совпадает с математическим ожиданием, что показывает естественность определения 3. Утверждение 3. Пусть Х – случайная величина, М(Х) – ее математическое ожидание, а – некоторое число. Тогда 1) М(а)=а; 2) М(Х-М(Х))=0; 3) М[(X-a)2]=M[(X-M(X))2]+(a-M(X))2. Для доказательства рассмотрим сначала случайную величину, являющуюся постоянной,
Если каждый член суммы разбивается на два слагаемых, то и вся сумма разбивается на две суммы, из которых первая составлена из первых слагаемых, а вторая – из вторых. Следовательно, математическое ожидание суммы двух случайных величин Х+У, определенных на одном и том же пространстве элементарных событий, равно сумме математических ожиданий М(Х) и М(У) этих случайных величин: М(Х+У) = М(Х) + М(У). А потому М(Х-М(Х)) = М(Х) - М(М(Х)). Как показано выше, М(М(Х)) = М(Х). Следовательно, М(Х-М(Х)) = М(Х) - М(Х) = 0. Поскольку (Х - а)2 = {(X – M(X)) + (M(X) - a)}2 = (X - M(X))2 + 2(X - M(X))(M(X) - a) + (M(X) – a)2, то M[(Х - а)2] =M(X - M(X))2 + M{2(X - M(X))(M(X) - a)} +M[(M(X) – a)2]. Упростим последнее равенство. Как показано в начале доказательства утверждения 3, математическое ожидание константы – сама эта константа, а потому M[(M(X) – a)2] = (M(X) – a)2. Поскольку постоянный множитель можно выносить за знак суммы, то M{2(X - M(X))(M(X) - a)} = 2(M(X) - a)М(X - M(X)). Правая часть последнего равенства равна 0, поскольку, как показано выше, М(Х-М(Х))=0.Следовательно, М[(X-a)2]=M[(X-M(X))2]+(a-M(X))2, что и требовалось доказать. Из сказанного вытекает, что М[(X-a)2] достигает минимума по а, равного M[(X-M(X))2], при а = М(Х), поскольку второе слагаемое в равенстве 3) всегда неотрицательно и равно 0 только при указанном значении а. Утверждение 4. Пусть случайная величина Х принимает значения х1, х2,…, хm, а f – некоторая функция числового аргумента. Тогда
Для доказательства сгруппируем в правой части равенства (4), определяющего математическое ожидание, члены с одинаковыми значениями
Пользуясь тем, что постоянный множитель можно выносить за знак суммы, и определением вероятности случайного события (2), получаем
что и требовалось доказать. Утверждение 5. Пусть Х и У – случайные величины, определенные на одном и том же пространстве элементарных событий, а и b – некоторые числа. Тогда M(aX+bY)=aM(X)+bM(Y). С помощью определения математического ожидания и свойств символа суммирования получаем цепочку равенств:
Требуемое доказано. Выше показано, как зависит математическое ожидание от перехода к другому началу отсчета и к другой единице измерения (переход Y=aX+b), а также к функциям от случайных величин. Полученные результаты постоянно используются в технико-экономическом анализе, при оценке финансово-хозяйственной деятельности предприятия, при переходе от одной валюты к другой во внешнеэкономических расчетах, в нормативно-технической документации и др. Рассматриваемые результаты позволяют применять одни и те же расчетные формулы при различных параметрах масштаба и сдвига. Независимость случайных величин – одно из базовых понятий теории вероятностей, лежащее в основе практических всех вероятностно-статистических методов принятия решений. Определение 4. Случайные величины Х и У, определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых чисел а и b независимы события {X=a} и {Y=b}. Утверждение 6. Если случайные величины Х и У независимы, а и b – некоторые числа, то случайные величины X+a иY+b также независимы. Действительно, события {X+a=с} и {Y+b=d} совпадают с событиями {X=с-a} и {Y=d-b} соответственно, а потому независимы. Пример 7. Случайные величины, определенные по результатам различных испытаний в схеме независимых испытаний, сами независимы. Это вытекает из того, что события, с помощью которых определяется независимость случайных величин, определяются по результатам различных испытаний, а потому независимы по определению независимых испытаний. В вероятностно-статистических методах принятия решений постоянно используется следующий факт: если Х и У – независимые случайные величины, f(X) и g(Y) – случайные величины, полученные из Х и У с помощью некоторых функций f и g, то f(X) и g(Y) – также независимые случайные величины. Например, если Х и У независимы, то Х2 и 2У+3 независимы, logX и logУ независимы. Доказательство рассматриваемого факта – тема одной из контрольных задач в конце главы. Подавляющее большинство вероятностно-статистических моделей, используемых на практике, основывается на понятии независимых случайных величин. Так, результаты наблюдений, измерений, испытаний, анализов, опытов обычно моделируются независимыми случайными величинами. Часто считают, что наблюдения проводятся согласно схеме независимых испытаний. Например, результаты финансово-хозяйственной деятельности предприятий, выработка рабочих, результаты (данные) измерений контролируемого параметра у изделий, отобранных в выборку при статистическом регулировании технологического процесса, ответы потребителей при маркетинговом опросе и другие типы данных, используемых при принятии решений, обычно рассматриваются как независимые случайные величины, вектора или элементы. Причина такой популярности понятия независимости случайных величин состоит в том, что к настоящему времени теория продвинута существенно дальше для независимых случайных величин, чем для зависимых. Часто используется следующее свойство независимых случайных величин. Утверждение 7. Если случайные величины Х и У независимы, то математическое ожидание произведения ХУ равно произведению математических ожиданий Х и У, т.е. М(ХУ)=М(Х)М(У). Доказательство. Пусть Х принимает значения х1, х2,…, хm, в то время как У принимает значения у1, у2,…, уk.Сгруппируем в задающей М(ХУ) сумме члены, в которых Х и У принимают фиксированные значения:
Поскольку постоянный множитель можно вынести за знак суммы, то
Из последнего равенства и определения вероятности события заключаем, что равенство (6) можно преобразовать к виду
Так как Х и У независимы, то
заключаем, что
Из равенства (5) следует, что первый сомножитель в правой части (7) есть М(Х), а второй – М(У), что и требовалось доказать. Пример 8. Построим пример, показывающий, что из равенства М(ХУ)=М(Х)М(У) не следует независимость случайных величин Х и У. Пусть вероятностное пространство состоит из трех равновероятных элементов
Тогда ХУ = Х, М(Х) = М(ХУ) = 0, следовательно, М(ХУ) = М(Х)М(У). Однако при этом Р(Х=0) = Р(У=0) = Р(Х=0, У=0) = Независимость нескольких случайных величин X, Y, Z,… означает по определению, что для любых чисел x, y, z,… справедливо равенство P(X=x, Y=y, Z=z,…) = P(X=x) P(Y=y) P(Z=z)… Например, если случайные величины определяются по результатам различных испытаний в схеме независимых испытаний, то они независимы. Дисперсия случайной величины. Математическое ожидание показывает, вокруг какой точки группируются значения случайной величины. Необходимо также уметь измерить изменчивость случайной величины относительно математического ожидания. Выше показано, что M[(X-a)2] достигает минимума по а при а = М(Х). Поэтому за показатель изменчивости случайной величины естественно взять именно M[(X-М(Х))2]. Определение 5. Дисперсией случайной величины Х называется число Установим ряд свойств дисперсии случайной величины, постоянно используемых в вероятностно-статистических методах принятия решений. Утверждение 8. Пусть Х – случайная величина, а и b – некоторые числа, Y = aX + b. Тогда D(Y) = a2D(X). Как следует из утверждений 3 и 5, M(Y) = aM(X) + b. Следовательно, D(Y) =M[(Y - M(Y))2] = M[(aX + b - aM(X) -b)2] = M[a2(X - M(X))2]. Поскольку постоянный множитель можно выносить за знак суммы, то M[a2(X - M(X))2] = a2M[(X - M(X))2] = a2 D(Х). Утверждение 8 показывает, в частности, как меняется дисперсия результата наблюдений при изменении начала отсчета и единицы измерения. Оно дает правило преобразования расчетных формул при переходе к другим значениям параметров сдвига и масштаба. Утверждение 9. Если случайные величины Х и У независимы, то дисперсия их суммы Х+У равна сумме дисперсий:D(X+Y) = D(X) + D(Y). Для доказательства воспользуемся тождеством (Х+У–(М(Х)+М(У))2 = (Х–М(Х))2 + 2(Х–М(Х))(У–М(У)) + (У–М(У))2, которое вытекает из известной формулы элементарной алгебры (a+b)2 = a2 + 2ab + b2 при подстановке a = X-M(X) и b= Y-M(Y). Из утверждений 3 и 5 и определения дисперсии следует, что D(X+Y) = D(X) + D(Y) + 2M{(Х–М(Х))(У–М(У))}. Согласно утверждению 6 из независимости Х и У вытекает независимость Х-М(Х) и У-М(У). Из утверждения 7 следует, что M{(Х–М(Х))(У–М(У))}= M(Х–М(Х))М(У–М(У)). Поскольку M(Х–М(Х)) = 0 (см. утверждение 3), то правая часть последнего равенства равна 0, откуда с учетом двух предыдущих равенств и следует заключение утверждения 9. Утверждение 10. Пусть X1, X2,…, Xk – попарно независимые случайные величины (т.е. Xi и Xj независимы, если Соотношения, сформулированные в утверждении 10, являются основными при изучении выборочных характеристик, поскольку результаты наблюдений или измерений, включенные в выборку, обычно рассматриваются в математической статистике, теории принятия решений и эконометрике как реализации независимых случайных величин. Для любого набора числовых случайных величин (не только независимых) математическое ожидание их суммы равно сумме их математических ожиданий. Это утверждение является обобщением утверждения 5. Строгое доказательство легко проводится методом математической индукции. При выводе формулы для дисперсии D(Yk) воспользуемся следующим свойством символа суммирования:
Положим ai = Xi – M(Xi), получим
Воспользуемся теперь тем, что математическое ожидание суммы равно сумме математических ожиданий:
Как показано при доказательстве утверждения 9, из попарной независимости рассматриваемых случайных величин следует, что Полученные в утверждениях 8-10 фундаментальные свойства таких характеристик случайных величин, как математическое ожидание и дисперсия, постоянно используются практически во всех вероятностно-статистических моделях реальных явлений и процессов. Пример 9. Рассмотрим событие А и случайную величину Х такую, что Воспользуемся формулой (5) для математического ожидания. Случайная величина Х принимает два значения – 0 и 1, значение 1 с вероятностью Р(А) и значение 0 с вероятностью 1 – Р(А), а потому М(Х) = 1 х Р(А) + 0 х (1 - Р(А)) = Р(А). Аналогично (Х – М(Х))2 = (1 – Р(А))2 с вероятностью Р(А) и (Х – М(Х))2 = (0 – Р(А))2 с вероятностью 1 – Р(А), а потому D(A) = (1 – P(A))2 P(A) + (P(A))2(1 – P(A)). Вынося общий множитель, получаем, что D(A) = P(A)(1 –P(A)). Пример 10. Рассмотрим k независимых испытаний, в каждом из которых некоторое событие А может наступить, а может и не наступить. Введем случайные величины X1, X2,…, Xk следующим образом: Случайная величина В = X1+ X2+…+ Xk называется биномиальной. Ясно, что 0<B<k при всех возможных исходах опытов. Чтобы найти распределение В, т.е. вероятности Р(В = а) при а = 0, 1, …, k, достаточно знать р – вероятность наступления рассматриваемого события в каждом из опытов. Действительно, случайное событие В = а осуществляется тогда и только тогда, когда событие А наступает ровно при а испытаниях. Если известны номера всех этих испытаний (т.е. номера в последовательности испытаний), то вероятность одновременного осуществления в а опытах события А и в k-а опытах противоположного ему – это вероятность произведения k независимых событий. Вероятность произведения равна произведению вероятностей, т.е. ра(1 - р)k-a. Сколькими способами можно задать номера аиспытаний из k? Это
где символом k! обозначено произведение всех натуральных чисел от 1 до k, т.е.
Название «биномиальное распределение» основано на том, что Р(В = а) является членом с номером (а+1) в разложении по биному Ньютона
если положить А = 1 – р, С = р. Тогда при j = a получим
Для числа сочетаний из k элементов по а, кроме Из утверждения 10 и расчетов примера 9 следует, что для случайной величины В, имеющей биномиальное распределение, математическое ожидание и дисперсия выражаются формулами
поскольку В является суммой k независимых случайных величин с одинаковыми математическими ожиданиями и дисперсиями, найденными в примере 9. Неравенства Чебышёва. Во введении к разделу обсуждалась задача проверки того, что доля дефектной продукции в партии равна определенному числу. Для демонстрации вероятностно-статистического подхода к проверке подобных утверждений являются полезными неравенства, впервые примененные в теории вероятностей великим русским математиком Пафнутием Львовичем Чебышёвым (1821-1894) и потому носящие его имя. Эти неравенства широко используются в теории математической статистики, а также непосредственно применяются в ряде практических задач принятия решении. Например, в задачах статистического анализа технологических процессов и качества продукции в случаях, когда явный вид функции распределения результатов наблюдений не известен (см. ниже, где, в частности, они применяются в задаче исключения резко отклоняющихся результатов наблюдений). Первое неравенство Чебышева. Пусть Х – неотрицательная случайная величина (т.е.
Доказательство. Все слагаемые в правой части формулы (4), определяющей математическое ожидание, в рассматриваемом случае неотрицательны. Поэтому при отбрасывании некоторых слагаемых сумма не увеличивается. Оставим в сумме только те члены, для которых
Для всех слагаемых в правой части (9)
Из (9) и (10) следует требуемое. Второе неравенство Чебышева. Пусть Х – случайная величина. Для любого положительного числа а справедливо неравенство
Это неравенство содержалось в работе П.Л.Чебышёва «О средних величинах», доложенной Российской академии наук 17 декабря 1866 г. и опубликованной в следующем году. Для доказательства второго неравенства Чебышёва рассмотрим случайную величину У = (Х – М(Х))2. Она неотрицательна, и потому для любого положительного числа b, как следует из первого неравенства Чебышёва, справедливо неравенство
Положим b = a2. Событие {Y>b} совпадает с событием {|X – M(X)|>a}, а потому
что и требовалось доказать. Пример 11. Можно указать неотрицательную случайную величину Х и положительное число а такие, что первое неравенство Чебышёва обращается в равенство. Достаточно рассмотреть Следовательно, первое неравенство Чебышёва в его общей формулировке не может быть усилено. Однако для подавляющего большинства случайных величин, используемых при вероятностно-статистическом моделировании процессов принятия решений, левые части неравенств Чебышёва много меньше соответствующих правых частей. Пример 12. Может ли первое неравенство Чебышёва обращаться в равенство при всех а? Оказывается, нет. Покажем, что для любой неотрицательной случайной величины с ненулевым математическим ожиданием можно найти такое положительное число а, что первое неравенство Чебышёва является строгим. Действительно, математическое ожидание неотрицательной случайной величины либо положительно, либо равно 0. В первом случае возьмем положительное а, меньшее положительного числа М(Х), например, положим а = М(Х)/2. Тогда М(Х)/а больше 1, в то время как вероятность события не может превышать 1, а потому первое неравенство Чебышева является для этого а строгим. Второй случай исключается условиями примера 11. Отметим, что во втором случае равенство 0 математического ожидания влечет тождественное равенство 0 случайной величины. А для такой случайной величины при любом положительном а и левая и правая части первого неравенства Чебышёва равны 0. Можно ли в формулировке первого неравенства Чебышева отбросить требование неотрицательности случайной величины Х? А требование положительности а? Легко видеть, что ни одно из двух требований не может быть отброшено, поскольку иначе правая часть первого неравенства Чебышева может стать отрицательной. Закон больших чисел. Неравенство Чебышёва позволяет доказать замечательный результат, лежащий в основе математической статистики – закон больших чисел. Из него вытекает, что выборочные характеристики при возрастании числа опытов приближаются к теоретическим, а это дает возможность оценивать параметры вероятностных моделей по опытным данным. Без закона больших чисел не было бы Теорема Чебышёва. Пусть случайные величины Х1, Х2,…, Хk попарно независимы и существует число С такое, чтоD(Xi)<C при всех i = 1, 2, …, k. Тогда для любого положительного
Доказательство. Рассмотрим случайные величины Yk = Х1 + Х2+…,+ Хk и Zk = Yk/k. Тогда согласно утверждению 10 М(Yk) = М(Х1)+М(Х2)+…+М(Хk), D(Yk) = D(Х1)+D(Х2)+…+D(Хk). Из свойств математического ожидания следует, что М(Zk) = М(Yk)/k, а из свойств дисперсии - что D(Zk) = D(Yk)/k2. Таким образом, М(Zk) ={М(Х1)+М(Х2)+…+М(Хk)}/k, D(Zk) ={D(Х1)+D(Х2)+…+D(Хk)}/k2. Из условия теоремы Чебышёва, что
Применим к Zk второе неравенство Чебышёва. Получим для стоящей в левой части неравенства (11) вероятности оценку
что и требовалось доказать. Эта теорема была получена П.Л.Чебышёвым в той же работе 1867 г. «О средних величинах», что и неравенства Чебышёва. Пример 13. Пусть С = 1, В рассматриваемом случае правая часть неравенства (11) равно 100/ k. Она не превосходит 0,1, если k не меньше 1000, не превосходит 0,05, если k не меньше 2000, не превосходит 0,00001, если k не меньше 10 000 000. Правая часть неравенства (11), а вместе с ней и левая, при возрастании k и фиксированных С и Наиболее важен для вероятностно-статистических методов принятия решений (и для математической статистики в целом) случай, когда все Xi , i = 1, 2, …, имеют одно и то же математическое ожидание M(X1) и одну и ту же дисперсию
Из закона больших чисел следует, что
Здесь знак В начале главы отмечалось, что с точки зрения ряда естествоиспытателей вероятность события А – это число, к которому приближается отношение количества осуществлений события А к количеству всех опытов при безграничном увеличении числа опытов. Известный математики Якоб Бернулли (1654-1705), живший в городе Базель в Швейцарии, в самом конце XVII века доказал это утверждение в рамках математической модели (опубликовано доказательство было лишь после его смерти, в 1713 году). Современная формулировка теоремы Бернулли такова. Теорема Бернулли. Пусть m – число наступлений события А в k независимых (попарно) испытаниях, и р есть вероятность наступления события А в каждом из испытаний. Тогда при любом
Доказательство. Как показано в примере 10, случайная величина m имеет биномиальное распределение с вероятностью успеха р и является суммой k независимых случайных величин Xi, i = 1, 2. …, k, каждое из которых равно 1 с вероятностью р и 0 с вероятностью 1-р, т.е. m= X1+ X2+…+ Xk .Применим к X1, X2,…, Xk теорему Чебышёва с С = р(1 - р) и получим требуемое неравенство (12). Теорема Бернулли дает возможность связать математическое определение вероятности (по А.Н.Колмогорову) с определением ряда естествоиспытателей (по Р.Мизесу (1883-1953)), согласно которому вероятность есть предел частоты в бесконечной последовательности испытаний. Продемонстрируем эту связь. Для этого сначала отметим, что
при всех р. Действительно,
Следовательно, в теореме Чебышёва можно использовать С = ј. Тогда при любом р и фиксированном Есть и прямые экспериментальные подтверждения того, что частота осуществления определенных событий близка к вероятности, определенной из теоретических соображений. Рассмотрим бросания монеты. Поскольку и герб, и решетка имеют одинаковые шансы оказаться сверху, то вероятность выпадения герба равна Ѕ из соображений равновозможности. Французский естествоиспытатель XVIII века Бюффон бросил монету 4040 раз, герб выпал при этом 2048 раз. Частота появления герба в опыте Бюффона равна 0,507. Английский статистик К.Пирсон бросил монету 12000 раз и при этом наблюдал 6019 выпадений герба – частота 0,5016. В другой раз он бросил монету 24000 раз, герб выпал 12012 раз – частота 0,5005. Как видим, во всех этих случаях частоты лишь незначительно отличаются от теоретической вероятности 0,5 [6, с.148]. О проверке статистических гипотез. С помощью неравенства (12) можно кое-что сказать по поводу проверки соответствия качества продукции заданным требованиям. Пусть из 100000 единиц продукции 30000 оказались дефектными. Согласуется ли это с гипотезой о том, что вероятность дефектности равна 0,23? Прежде всего, какую вероятностную модель целесообразно использовать? Принимаем, что проводится сложный опыт, состоящий из 100000 испытаний 100000 единиц продукции на годность. Считаем, что испытания (попарно) независимы и что в каждом испытании вероятность того, что единица продукции является дефектной, равна р. В реальном опыте получено, что событие «единица продукции не является годной» осуществилось 30000 раз при 100000 испытаниях. Согласуется ли это с гипотезой о том, что вероятность дефектностир = 0,23? Для проверки гипотезы воспользуемся неравенством (12). В рассматриваемом случае k = 100000, m = 30000, m/k = 0,3, p = 0,23, m/k – p = 0,07. Для проверки гипотезы поступают так. Оценим вероятность того, что m/k отличается от ртак же, как в рассматриваемом случае, или больше, т.е. оценим вероятность выполнения неравенства |m/k – 0,23| >0,07. Положим в неравенстве (12) р = 0,23,
При k = 100000 правая часть (13) меньше 1/2500. Значит, вероятность того, что отклонение будет не меньше наблюдаемого, весьма мала. Следовательно, если исходная гипотеза верна, то в рассматриваемом опыте осуществилось событие, вероятность которого меньше 1/2500. Поскольку 1/2500 – очень маленькое число, то исходную гипотезу надо отвергнуть. Подробнее методы проверки статистических гипотез будут рассмотрены ниже. Здесь отметим, что одна из основных характеристик метода проверки гипотезы – уровень значимости, т.е. вероятность отвергнуть проверяемую гипотезу (ее в математической статистике называют нулевой и обозначают Н0), когда она верна. Для проверки статистической гипотезы часто поступают так. Выбирают уровень значимости - малое число Насколько результат проверки гипотезы Н0 зависит от числа испытаний k? Пусть при k = 100, k = 1000, k = 10000 оказалось, что m = 30, m = 300, m = 3000 соответственно, так что во всех случаях m/k = 0,3. Какие значения принимает вероятность
и ее оценка – правая часть формулы (13)? При k = 100 правая часть (13) равна приблизительно 0,36, что не дает оснований отвергнуть гипотезу. При k = 1000 правая часть (13) равна примерно 0,036. Гипотеза отвергается на уровне значимости Более точные расчеты, основанные на применении центральной предельной теоремы теории вероятностей (см. ниже), дают Р100 = 0,095,Р1000 = 0,0000005, так что оценка (13) является в рассматриваемом случае весьма завышенной. Причина в том, что получена она из наиболее общих соображений, применительно ко всем возможным случайным величинам улучшить ее нельзя (см. пример 11 выше), но применительно к биномиальному распределению – можно. Ясно, что без введения уровня значимости не обойтись, ибо даже очень большие отклонения m/k от р имеют положительную вероятность осуществления. Так, при справедливости гипотезы Н0 событие «все 100000 единиц продукции являются дефектными» отнюдь не является невозможным с математической точки зрения, оно имеет положительную вероятность осуществления, равную 0,23100000, хотя эта вероятность и невообразимо мала. Аналогично разберем проверку гипотезы о симметричности монеты. Пример 14. Если монета симметрична, то р = Ѕ, где р – вероятность выпадения герба. Согласуется ли с этой гипотезой результат эксперимента, в котором при 10000 бросаниях выпало 4000 гербов? В рассматриваемом случае m/k = 0,4. Положим в неравенстве (12) р = 0,5, ε = 0,1:
При k = 10000 правая часть последнего неравенства равна 1/400. Значит, если исходная гипотеза верна, то в нашем единственном эксперименте осуществилось событие, вероятность которого весьма мала – меньше 1/400. Поэтому исходную гипотезу необходимо отвергнуть. Если из 1000 бросаний монеты гербы выпали в 400 случаях, то правая часть выписанного выше неравенства равна 1/40. Гипотеза симметричности отклоняется на уровне значимости 0,05 (и 0,1), но рассматриваемые методы не дают возможности отвергнуть ее на уровне значимости 0,01. Если k = 100, а m = 40, то правая часть неравенства равна ј. Оснований для отклонения гипотезы нет. С помощью более тонких методов, основанных на центральной предельной теореме теории вероятностей, можно показать, что левая часть неравенства равна приблизительно 0,05. Это показывает, как важно правильно выбрать метод проверки гипотезы или оценивания параметров. Следовательно, целесообразна стандартизация подобных методов, позволяющая сэкономить усилия, необходимые для сравнения и выбора наилучшего метода, а также избежать устаревших, неверных или неэффективных методов. Ясно, что даже по нескольким сотням опытов нельзя достоверно отличить абсолютно симметричную монету (р = Ѕ) от несколько несимметричной монеты (для которой, скажем, р = 0,49). Более того, любая реальная монета несколько несимметрична, так что монета с р = Ѕ - математическая абстракция. Между тем в ряде управленческих и производственных ситуаций необходимо осуществить справедливую жеребьевку, а для этого требуется абсолютно симметричная монета. Например, речь может идти об очередности рассмотрения инвестиционных проектов комиссией экспертов, о порядке вызова для собеседования кандидатов на должность, об отборе единиц продукции из партии в выборку для контроля и т.п. Пример 15. Можно ли с помощью несимметричной монеты получить последовательность испытаний с двумя исходами, каждый из которых имеет вероятность 1/2 ? Ответ: да, можно. Приведем способ, предложенный видным польским математиком Гуго Штейнгаузом (1887-1972). Будем бросать монету два раза подряд и записывать исходы бросаний так (Г – герб, Р – решетка, на первом месте стоит результат первого бросания, на втором – второго): ГР запишем как Г, в то время РГ запишем как Р, а ГГ и РР вообще не станем записывать. Например, если исходы бросаний окажутся такими: ГР, РГ, ГР, РР, ГР, РГ, ГГ, РГ, РР, РГ, то запишем их в виде: Г, Р, Г, Г, Р, Р, Р. Сконструированная таким образом последовательность обладает теми же свойствами, что и полученная при бросании идеально симметричной монеты, поскольку даже у несимметричной монеты последовательность ГР встречается столь же часто, как и последовательность РГ. Применим теорему Бернулли и неравенство (12) к обработке реальных данных. Пример 16. С 1871 г. по 1900 г. в Швейцарии родились 1359671 мальчик и 1285086 девочек. Совместимы ли эти данные с предположением о том, что вероятность рождения мальчика равна 0,5? А с предположением, что она равна 0,515? Другими словами, требуется проверить нулевые гипотезы Н0: р = 0,5 и Н0: р = 0,515 с помощью неравенства (12). Число испытаний равно общему числу рождений, т.е. 1359671 + 1285086 = 2644757. Есть все основания считать испытания независимыми. Число рождений мальчиков составляет приблизительно 0,514 всех рождений. В случае р = Ѕ имеем ε = 0,014, и правая часть неравенства (12) имеет вид
Таким образом, гипотезу р = 0,5 следует считать несовместимой с приведенными в условии данными. В случае р = 0,515 имеем ε = 0,001, и правая часть (12) равна приблизительно 0,1, так что с помощью неравенства (12) отклонить гипотезу Н0: р = 0,515 нельзя. Итак, здесь на основе элементарной теории вероятностей (с конечным пространством элементарных событий) мы сумели построить вероятностные модели для описания проверки качества деталей (единиц продукции) и бросания монет и предложить методы проверки гипотез, относящихся к этим явлениям. В математической статистике есть более тонкие и сложные методы проверки описанных выше гипотез, которыми и пользуются в практических расчетах. Можно спросить: «В рассмотренных выше моделях вероятности были известны заранее – со слов Струкова или же из-за того, что мы предположили симметричность монеты. А как строить модели, если вероятности неизвестны? Как оценить неизвестные вероятности?» Теорема Бернулли – результат, с помощью которого дается ответ на этот вопрос. Именно, оценкой неизвестной вероятности р является число m/k, поскольку доказано, что при возрастании kвероятность того, что m/k отличается от p более чем на какое-либо фиксированное число, приближается к 0. Оценка будет тем точнее, чем больше k. Более того, можно доказать, что с некоторой точки зрения (см. далее) оценка m/k для вероятности р является наилучшей из возможных (в терминах математической статистики – состоятельной, несмещенной и эффективной).
|
|||||||||||||||||||||||
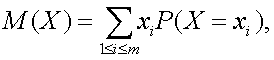 (5)
(5)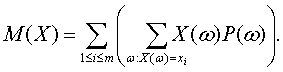
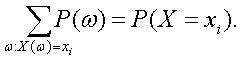
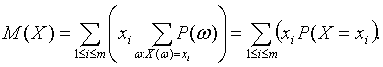
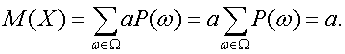
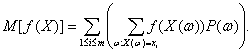
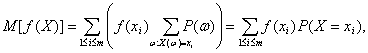
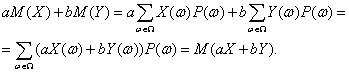
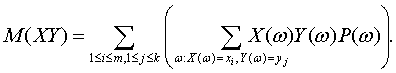 (6)
(6)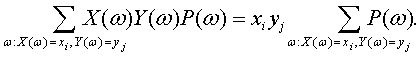
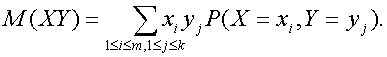
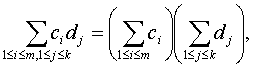
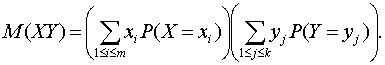 (7)
(7)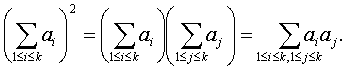
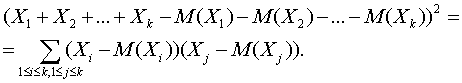
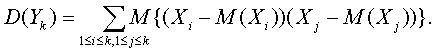 (8)
(8)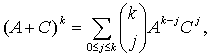
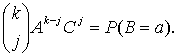
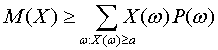 . (9)
. (9)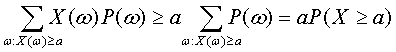 . (10)
. (10)