«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Теория принятия решений Учебное пособие. - М.: Издательство "Март", 2004. 2. ОПИСАНИЕ НЕОПРЕДЕЛЕННОСТЕЙ В ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ 2.3.5. Сравнение методов оценивания параметровВ теории оценивания параметров классической математической статистики установлено, что метод максимального правдоподобия, как правило, лучше (в смысле асимптотической дисперсии асимптотического среднего квадрата ошибки), чем метод моментов. Однако в интервальной статистике это, вообще говоря, не так, что продемонстрировано выше на примере оценивания параметров гамма-распределения. Сравним эти два метода оценивания в случае интервальных данных в общей постановке. Поскольку метод максимального правдоподобия – частный случай метода минимального контраста, начнем с разбора этого несколько более общего метода. Оценки минимального контраста. Пусть Х – пространство, в котором лежат независимые одинаково распределенные случайные элементы
Если множество Оценками минимального контраста являются, в частности, многие робастные статистики [3,36]. Эти оценки широко используются в статистике объектов нечисловой природы [3,27], поскольку при Пусть в Х имеется мера
то оценка минимального контраста переходит в оценку максимального правдоподобия. Асимптотическое поведение оценок минимального контраста в случае пространств Х и В рассматриваемой математической модели предполагается, что статистику известны лишь искаженные значения
Будем изучать величину Пусть
при всех
где Используя обозначения векторов x = (x1 , x2 , ..., xn ), y = (y1 , y2 , ..., yn ), введем суммы
Аналогичным образом введем функции B0(y), B1(y), R(y), в которых вместо xi стоят yi, i=1,2,…,n. Поскольку в соответствии с теоремой Ферма оценка минимального контраста
то, подставляя в (27) xi вместо x и суммируя по i = 1,2,…,n, получаем, что
откуда
Решения уравнения (28) будем также называть оценками минимального контраста. Хотя уравнение (28) – лишь необходимое условие минимума, такое словоупотребление не будет вызывать трудностей. Теорема 1. Пусть для любого x выполнено соотношение (27). Пусть для случайной величины х1 с распределением, соответствующим значению параметра
Тогда существуют оценки минимального контраста Доказательство. Возьмем
Тогда с вероятностью не менее
При
(см. формулу (29)). С вероятностью не менее
Если Теорема 2. Пусть выполнены условия теоремы 2 и, кроме того, для случайной величины х1, распределение которой соответствует значению параметра
Тогда оценка минимального контраста имеет асимптотически нормальное распределение:
для любого х, где Ф(x) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Доказательство. Из центральной предельной теоремы вытекает, что числитель в правой части формулы (30) асимптотически нормален с математическим ожиданием 0 и дисперсией Нотна оценки минимального контраста. Аналогично (30) нетрудно получить, что
Следовательно, Покажем, что при
Поскольку
Можно сказать, что наличие погрешностей В правой части (36) первое слагаемое – квадрат асимптотической нотны, второе соответствует статистической ошибке. Приравнивая их, получаем рациональный объем выборки
Остается доказать соотношение (35) и вычислить С. Укажем сначала условия, при которых Теорема 3. Пусть существуют константа
при всех x. Пусть для случайной величины х1, распределение которой соответствует Доказательство проведем по схеме доказательства теоремы 1. Из неравенств (37) вытекает, что
Возьмем
Тогда с вероятностью не менее
В силу (38) при этом
Пусть
Тогда с вероятностью не менее
Завершается доказательство дословным повторением такового в теореме 1, с единственным отличием – заменой в обозначениях x на y. Теорема 4. Пусть выполнены условия теоремы 3 и, кроме того, существуют математические ожидания (при
Тогда выполнено соотношение (35) с
Доказательство. Воспользуемся следующим элементарным соотношением. Пусть a и b – бесконечно малые по сравнению с Z и B соответственно. Тогда с точностью до бесконечно малых более высокого порядка
Чтобы применить это соотношение к анализу
При
с точностью до бесконечно малых более высокого порядка, где
Ясно, что задача оптимизации
имеет решение
при этом максимальное значение линейной формы есть
С целью упрощения правой части (42) воспользуемся тем, что
где
по вероятности, то второе слагаемое в (43) сходится к 0, а первое в силу закона больших чисел с учетом (39) сходится к СА2, где С определено в (40). Теорема 4 доказана. Оценки метода моментов. Пусть
Оценки метода моментов имеют вид
(функции g и hj должны удовлетворять некоторым дополнительным условиям [, с.80], которые здесь не приводим). Очевидно, что
с точностью до бесконечно малых более высокого порядка, а потому с той же точностью
Теорема 5. Пусть при
функция g дважды непрерывно дифференцируема в некоторой окрестности точки
причем Mt(x1) существует. Тогда
с точностью до бесконечно малых более высокого порядка, причем
Доказательство теоремы 5 сводится к обоснованию проведенных ранее рассуждений, позволивших получить формулу (45). В условиях теоремы 5 собраны предположения, достаточные для такого обоснования. Так, условие (46) дает возможность обосновать соотношения (44); существование Полученные в теоремах 4 и 5 нотны оценок минимального контраста и метода моментов, асимптотические дисперсии этих оценок (см. теорему 2 и [40] соответственно) позволяют находить рациональные объемы выборок, строить доверительные интервалы с учетом погрешностей измерений, а также сравнивать оценки по среднему квадрату ошибки (36). Подобное сравнение было проведено для оценок максимального правдоподобия и метода моментов параметров гамма-распределения. Установлено, что классический вывод о преимуществе оценок максимального правдоподобия [33, с.99-100] неверен в случае
|
||
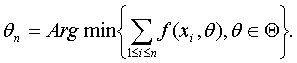
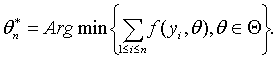
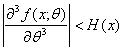
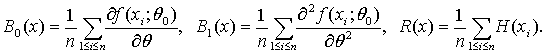
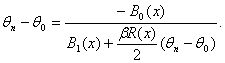 (30)
(30)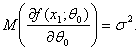
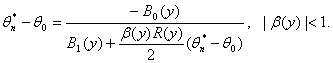 (34)
(34)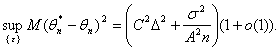 (36)
(36)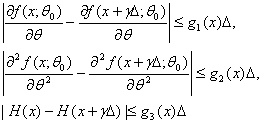 …(37)
…(37)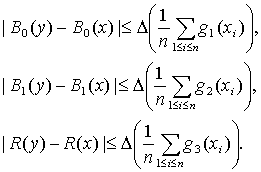 (38)
(38)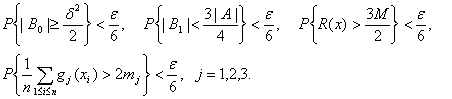
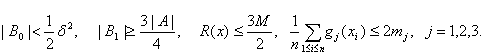
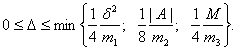
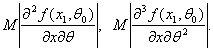 (39)
(39)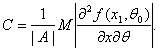 (40)
(40)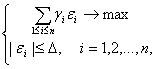 (41)
(41)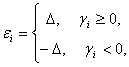
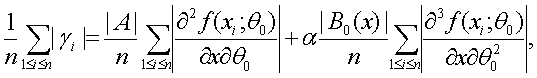 (43)
(43)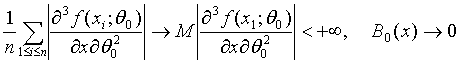
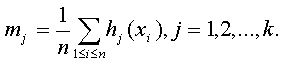
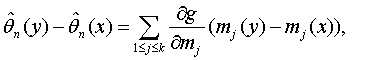
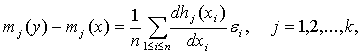 (44)
(44)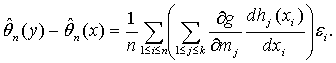 (45)
(45)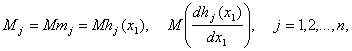
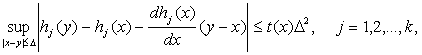 (46)
(46)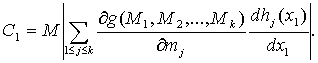
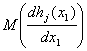 обеспечивает существование С1, и т.д. Завершает доказательство ссылка на решение задачи оптимизации (41) и применение закона больших чисел.
обеспечивает существование С1, и т.д. Завершает доказательство ссылка на решение задачи оптимизации (41) и применение закона больших чисел.