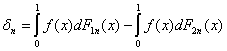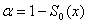«Управление и Оптимизация Производственного Предприятия»
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
М.: МЗ-Пресс, 2004. Глава 2. Статистические методы в пространствах произвольной природы 2.6. Статистики интегрального типа В прикладной статистике широко используются статистики типа омега-квадрат и типа Колмогорова-Смирнова [6]. Они применяются для проверки согласия с фиксированным распределением или семейством распределений, для проверки однородности двух выборок, симметрии распределения относительно 0, при оценивании условной плотности и регрессии в пространствах произвольной природы и т.д. Статистики интегрального типа и их асимптотика. Рассмотрим статистики интегрального типа
где Х – некоторое пространство, по которому происходит интегрирование (например, X = [0; 1], X = R1 или X = Rk). Здесь {α} – направленное множество, переход к пределу по которому обозначен как α→∞ (см. приложение 1). Случайные функции fα: XЧΩ → Y обычно принимают значения, являющиеся числами. Но иногда рассматривают и постановки, в которых У = Rk или У – банахово пространство (т.е. полное нормированное пространство [27]). Наконец, Fα(x,ω) – случайная функция распределения или случайная вероятностная мера; в последнем случае используют также обозначение dFα(x,ω)= Fα(dx,ω). Предполагаются выполненными необходимые для корректности изложения внутриматематические предположения измеримости, например, сформулированные в [28, 29]. Пример 1. Рассмотрим критерий Лемана – Розенблатта, т.е. критерий типа омега-квадрат для проверки однородности двух независимых выборок [6]. Его статистика имеет вид: LR = Fm(x) – Gn(x))2dHm+n(x) , где Fm(x) – эмпирическая функция распределения, построенная по первой выборке объема m, Gn(x)) - эмпирическая функция распределения, построенная по второй выборке объема n, а Hm+n(x) – эмпирическая функция распределения, построенная по объединенной выборке объема m+n. Легко видеть, что Hm+n(x) = Ясно, что статистика LR имеет вид (1). При этом х – действительное число, Х = У = R1, в роли α выступает пара (m, n), и α→∞ означает, что min(m, n) → ∞. Далее, fα(x,ω) = Наконец, Fα(x,ω) = Hm+n(x). Теперь обсудим асимптотическое поведение функций fα(x,ω) и Fα(x,ω), с помощью которых определяется статистика Лемана – Розенблатта LR. Ограничимся случаем, когда справедлива гипотеза однородности, т.е. совпадают функции распределения, соответствующие генеральным совокупностям, из которых взяты выборки. Их общую функцию распределения обозначим F(x). Она предполагается непрерывной. Введем в рассмотрение выборочные процессы
Нетрудно проверить, что
Сделаем замену переменной t = F(x). Тогда выборочные процессы переходят в соответствующие эмпирические процессы (см. приложение 1):
Конечномерные распределения этого процесса, т.е. распределения случайных векторов
для всех возможных наборов (t1, t2, … , tk), сходятся к конечномерным распределениям квадрата броуновского моста ξ2(t). В соответствии с разделом П-5 приложения 1 рассматриваемая сходимость по распределению обозначается так:
Нетрудно видеть, что при любом х Fα(x,ω) = Hm+n(x) → F(x) при α→∞ (сходимость по вероятности). С помощью замены переменной t = F(x) получаем, что Fα(F-1(t),ω) = Hm+n(F-1(t)) → t (3) при α→∞. Из соотношений (2) и (3) хотелось бы сделать вывод, что в случае статистики Лемана - Розенблатта типа омега-квадрат
т.е. предельным распределением этой статистики является классическое распределение [30], найденное как предельное для одновыборочной статистики критерия согласия омега-квадрат, известного также как критерий Крамера - Мизеса - Смирнова. Действительно, сформулированное утверждение справедливо. Однако доказательство нетривиально. Так, может показаться очевидным следующее утверждение. Утверждение 1. Пусть f: [0; 1] → R1 – ограниченная функция, Gn(x) и G(x) – функции распределения, Gn(0) =G(0) =0, Gn(1) = G(1) = 1, причем Gn(x) → G(x) при всех х. Тогда
Это утверждение неверно (ср. [31, с.42]). Действительно, пусть f(x) = 1, если х рационально, и f(x) = 0, если хиррационально, G(x) =x, а Gn(x) имеет скачки величиной 2-n в точках m/2n, m = 1, 2, … , 2n при всех n =1, 2, … ТогдаGn(x) → G(x) при всех х, однако
при всех n =1, 2, … Следовательно, вопреки сформулированному выше утверждению 1,
т.е. соотношение (4) неверно. Итак, сформулируем проблему. Пусть известно, что последовательность случайных функций fα(x, ω) сходится по распределению при α→∞ к случайной функции f(x,ω). Пусть последовательность случайных мер Fα(A,ω), определенных на множествах А из достаточно обширного семейства, сходится по распределению к вероятностной мереF(A) при α→∞. Если речь идет о конечномерном пространстве и меры задаются функциями распределения, то сходимость Fα(х,ω) к F(х) должна иметь место во всех точках непрерывности F(х). В каких случаях можно утверждать, что при α→∞ справедлив предельный переход
Выше показано, что, например, ограниченности fα(x, ω) для этого недостаточно. Метод аппроксимации ступенчатыми функциями. Рассмотрим общий метод, позволяющий получить предельные распределения не только для статистик интегрального типа, но и для других статистических критериев, например, для критериев типа Колмогорова. Пусть T = {С1, С2, … , Сk} – разбиение пространства Х на непересекающиеся подмножества. Пусть в каждом элементе Сj разбиения T выделена точка xj, j = 1, 2, … , k. На множестве функций f: X → Y введем оператор AT: если x ATf(x) = f(xj), j = 1, 2, … . k. (5) Тогда ATf – аппроксимация функции f ступенчатыми (кусочно-постоянными) функциями. Пусть fα(x,ω) – последовательность случайных функций на Х, а К(∙) – функционал на множестве всех возможных их траекторий как функций от х. Для изучения распределения К(fα) методом аппроксимации ступенчатыми функциями используют разложение К(fα) = К(АТfα) + {К(fα) - К(АТfα)}. (6) Согласно (5) распределение первого слагаемого в (6) определяется конечномерным распределением случайного элемента, а именно, распределением вектора (fα(x1,ω), fα(x2,ω), … fα(xk,ω)). (7) В обычных постановках предельной теории классических непараметрических критериев распределение вектора (7) сходится при α→∞ к соответствующему конечномерному распределению предельной случайной функции f(x,ω), т.е. к распределению случайного вектора (f(x1,ω), f(x2,ω), … f(xk,ω)). (8) В соответствии с теорией наследования сходимости (приложение 1) при слабых условиях на функционал К(∙) из сходимости по распределению вектора (7) к вектору (8) следует сходимость по распределению К(АТfα) к К(АТf). Используя аналогичное (6) разложение К(f) = К(АТf) + {К(f) - К(АТf)}, (9) можно устанавливать сходимость по распределению К(fα) к К(f) при α→∞ в два этапа: сначала выбрать разбиение Ттак, чтобы вторые слагаемые в правых частях соотношений (6) и (9) были малы, а затем при фиксированном оператореАТ воспользоваться сходимостью по распределению К(АТfα) к К(АТf). Рассмотрим простой пример применения метода аппроксимации ступенчатыми функциями. Обобщение теоремы Хелли. Пусть f: [0; 1] → R1 – измеримая функция, Fn(x) – функции распределений, сосредоточенных на отрезке [0; 1]. Пусть Fn(x) сходятся в основном к функции распределения F(x), т.е.
для всех х, являющихся точками непрерывности F(x). Утверждение 2. Если f(x) – непрерывная функция, то
(рассматриваются интегралы Лебега-Стилтьеса). Утверждение 2 известно в литературе как первая теорема Хелли [27, с.344-346], вторая теорема Хелли [32, с.174-175], лемма Хелли-Брея [33, с.193-194]. Естественно поставить вопрос: при каких f из (10) следует (11)? Необходимо ввести условия и на Fn: если Fn ≡F, то соотношение (11) верно для любой измеримой функции f, для которой интеграл в (11) существует. Поэтому рассмотрим следующую постановку. Постановка 1. Пусть функция f такова, что для любой последовательности Fn, удовлетворяющей (10), справедливо (11). Что можно сказать о функции f? В работах [28, 29] найдены следующие необходимые и достаточные условия на функцию f. Теорема 1. Пусть ограниченная на [0; 1] функция f интегрируема по Риману-Стилтьесу по функции распределения F(x). Тогда для любой последовательности функций распределения Fn, сходящейся в основном к F, имеет место предельный переход (11). Теорема 2. Пусть функция f не интегрируема по Риману-Стилтьесу по функции распределения F(x). Тогдасуществует последовательность функций распределения Fn, сходящаяся в основном к F, для которой соотношение (11) не выполнено. Теоремы 1 и 2 в совокупности дают необходимые и достаточные условия для f в постановке 1. А именно, необходимо и достаточно, чтобы ограниченная на [0; 1] функция f была интегрируема по Риману-Стилтьесу по F. Напомним определение интегрируемости функции f по Риману-Стилтьесу по функции распределения F [27, с.341]. Рассмотрим разбиение T = {С1, С2, … , Сk}, где Сi = [yi-1, yi), i = 1, 2, …, m – 1, Сm = [ym-1, ym], (12) 0 = y0 < y1 < y2 <…< ym = 1. Выберем в Сi произвольную точку xi, i = 1, 2, …, m, и составим сумму
Если при max(yi – yi-1) → 0 эти суммы стремятся к некоторому пределу (не зависящему ни от способа дробления отрезка [0; 1], ни от выбора точек xi в каждом из элементов разбиения), то этот предел называется интегралом Римана-Стилтьеса от функции f по функции F по отрезку [0; 1] и обозначается символом, приведенным в правой части равенства (11). Рассмотрим суммы Дарбу-Стилтьеса
где
Ясно, что SH(T) < S(T) < SB(T). Необходимым и достаточным условием интегрируемости по Риману-Стилтьесу является следующее: для любой последовательности разбиений Tk, k = 1, 2, 3, … вида (12) такой, что max(yi – yi-1) → 0 при k→∞, имеем
Напомним, что согласно разделу П-3 приложения 1 колебанием δ(f, B) функции f на множестве B называется δ(f, B) = sup{|f(x) – f(y)|, x δ(f, Сi) = Mi – mi, то условие (13) можно записать в виде
Условие (14), допускающее обобщение с Х = [0; 1] и f: [0; 1] → R1 на X и f более общего вида, и будем использовать при доказательстве теорем 1 и 2. Доказательство теоремы 1. Согласно методу аппроксимации ступенчатыми функциями рассмотрим операторАТ. Как легко проверить, имеет место разложение
Поскольку |f(x) - ATf(x)| < δ(f, Xi), x то первое слагаемое в правой части (15) не превосходит
а второе не превосходит
Согласно определению оператора АТ третье слагаемое в (15) имеет вид
Очевидно, оно не превосходит по модулю
(здесь используется ограниченность f на X). Согласно (16) первое слагаемое в правой части (15) не превосходит
Поскольку
то первое слагаемое в правой части (15) не превосходит
Из оценок, относящихся к трем слагаемым в разложении (15), следует, что
Используя оценку (17), докажем, что βn → 0 при n → ∞. Пусть дано ε > 0. Согласно условию интегрируемости функции f по Риману-Стилтьесу, т.е. условию (14), можно указать разбиение T = T(ε) такое, что
и в точках yi, i = 1, 2, …, m - 1 (см. (12)), функция F непрерывна. Поскольку Fn(Xi) = Fn(yi) - Fn(yi-1), то из (10) следует, что существует число n = n(ε) такое, что при n > n(ε) справедливо неравенство
Из (17), (18) и (19) следует, что при n > n(ε) справедливо неравенство
что и требовалось доказать. Обсудим условие ограниченности f. Если оно не выполнено, то из (10) не всегда следует (11). Пример 2. Пусть f(x) = 1/x при x > 0 и f(0)=0. Пусть F(0,5) = 0, т.е. предельное распределение сосредоточено на [1/2; 1]. Пусть распределение Fn на [0; Ѕ) имеет единственный атом в точке x = 1/n величиной n-1/2, а на [1/2; 1] справедливо (10). Тогда по причинам, изложенным при доказательстве теоремы 1,
однако
т.е. соотношение (11) не выполнено. Условие ограниченности подынтегральной функции f можно заменить, как это сделано, например, в [28], на условие строгого возрастания функции распределения F. Лемма. Пусть функции распределения F всюду строго возрастает, т.е. из x1 < x2 вытекает F(x1) < F(x2). Пусть функция f интегрируема по Риману-Стилтьесу по F, т.е. выполнено (14). Тогда функция f ограничена. Доказательство. Рассмотрим точки 0 = y0 < y1 < y2 <…< y2m = 1 и два разбиения
Тогда для любых двух точек х и х′ можно указать конечную последовательность точек x1 = x, x2, x3, …, xs, xs+1 = x′ такую, что любые две соседние точки xi, xi+1, i = 1, 2, …, s, одновременно принадлежат некоторому элементу Ciразбиения T1 или разбиения T2, причем Сi ≠ Сj при i ≠ j. Действительно, пусть Из указанных выше свойств последовательности x1 = x, x2, x3, …, xs, xs+1 = x′ следует, что
Пусть теперь число max(yi – yi-2) настолько мало, что согласно (14)
Тогда согласно двум последним соотношениям
что и доказывает лемму. Доказательство теоремы 2. Пусть условие (14) не выполнено, т.е. существуют число γ > 0 и последовательность разбиений Tn, n = 1, 2, …, такие, что max(yi – yi-1) → 0 при n→∞ и при всех n
Для доказательства теоремы построим две последовательности функций распределения F1n и F2n, n = 1, 2, …, для которых выполнено (10), но последовательность
не стремится к 0 при n → ∞. Тогда (11) не выполнено хотя бы для одной из последовательностей F1n и F2n. Для любого С – элемента некоторого разбиения Т – можно указать, как вытекает из определения δ(f, C), точкиx1(C) и x2(C) такие, что f (x1(C)) - f(x2(C)) > Ѕ δ(f, C). (21) Построим F1n и F2n следующим образом. Пусть F1n(С) = F2n(С) = F(С) для любого С из Tn. При этом F1nимеет в С один атом в точке x1(C) величиной F(С), а F2n имеет в С также один атом в точке x2(C) той же величиныF(С). Другими словами, распределение F1n в С сосредоточено в одной точке, а именно, в x1(C), а распределение F2nсосредоточено в x2(C). Тогда
Из (20), (21) и (22) следует, что
Остается показать, что для последовательностей функций распределения F1n и F2n выполнено (10). Пусть х – точка непрерывности F. Пусть y1(x, T) = max{ykn: ykn < x}, y2(x, T) = min{ ykn: ykn > x}, где ykn – точки, определяющие разбиения Tn согласно (12). В соответствии с определением Fin Fin(yj(x, Tn))= F(yj(x, Tn)), i = 1, 2, j = 1, 2, а потому |Fin(x) – F(x)| < F(y2(x, Tn)) - F(y1(x, Tn)), i = 1, 2. В силу условия max(ykn – y(k-1)n) → 0 и непрерывности F в точке x правая часть последнего соотношения стремится к 0 при n → ∞, что и заканчивает доказательство теоремы 2. Теоремы 1 и 2 демонстрируют основные идеи предельной теории статистик интегрального типа и непараметрических критериев в целом. Как показывают эти теоремы, основную роль в рассматриваемой теории играет предельное соотношение (14). Отметим, что если δ(f, Tn) → 0 при n → ∞, то (14) справедливо, но, вообще говоря, не наоборот. Естественно возникает еще ряд постановок. Пусть (14) выполнено для f1 и f2. При каких функциях h это соотношение выполнено для h(x, f1(x), f2(x))? В прикладной статистике вместо f(x) рассматривают fα(x, ω) и f(x, ω), а вместо интегрирования по функциям распределения Fn(x) – интегрирование по случайным мерам Fα(ω). Как меняются формулировки в связи с такой заменой? В связи со слабой сходимостью (т.е. сходимостью по распределению) ATfα к AT и переходом от fα(x, ω) к hα(x, f1α(x, ω), f2α(x, ω)) возникает следующая постановка. Пусть κα слабо сходится к κ при α→∞. Когда распределения gα(κα) сближаются с распределениями gα(κ)? Полным ответом на последний вопрос являются необходимые и достаточные условия наследования сходимости. Они приведены в приложении 1. Основные результаты. Наиболее общая теорема типа теоремы 1 выглядит так [29]. Теорема 3. Пусть существует последовательность разбиений Tn, n = 1, 2, …, такая, что при n →∞ и α→∞
Пусть для любого С, входящего хотя бы в одно из разбиений Tn, Fα(C, ω) → F(C) (24) при α→∞ (сходимость по вероятности). Пусть fα асимптотически ограничены по вероятности при α→∞. Тогда
при α→∞ (сходимость по вероятности). Как известно, полное сепарабельное метрическое пространство называется польским. Это понятие понадобится для формулировки аналога теоремы 2. Теорема 4. Пусть Х – польское пространство, У конечномерно, существует измельчающаяся последовательность Tn разбиений, для которой соотношение (23) не выполнено. Тогда существует удовлетворяющая (24) последовательность Fα, для которой соотношение (25) неверно, хотя Fα слабо сходится к F при α→∞. Условие (23) естественно назвать условием римановости, поскольку в случае, рассмотренном в теореме 1, оно является условием интегрируемости по Риману-Стилтьесу. Рассмотрим наследуемость римановости при переходе отf1α(x, ω) со значениями в У1 и f2α(x, ω) со значениями в У2, удовлетворяющих (23), к hα(x, f1α(x, ω), f2α(x, ω)) со значениями в У3. Положим
где ||∙||k – норма (т.е. длина вектора) в пространстве Yk, k = 1, 2. Рассмотрим также множества
и функции
Наконец, понадобится измеритель колеблемости
и множество
Теорема 5. Пусть функции hα асимптотически (при α→∞) ограничены на множестве Z(a) при любом положительном a. Пусть функции f1α и f2α асимптотически ограничены по вероятности и удовлетворяют условию (23). Пусть для участвующей в (23) последовательности Tn c(hα, Tn, a, ε) → 0 (26) при α→∞, n→∞, ε→ 0 и любом положительном a. Тогда функции f3α(x, ω) = hα(x, f1α(x, ω), f2α(x, ω)) удовлетворяют условию (23) и асимптотически ограничены по вероятности. Теорема 6. Пусть условие (26) не выполнено для hα. Тогда существуют детерминированные ограниченные функции f1α и f2α такие, что соотношение (23) выполнено для f1α и f2α и не выполнено для f3α. Пример 3. Пусть X = [0; 1]k, пространства Y1 и Y2 конечномерны, функция hα ≡ h(x, y1, y2) непрерывна. Тогда условие (26) выполнено. С помощью теорем 3 и 5 и результатов о наследовании сходимости можно изучить асимптотическое поведение статистик интегрального типа
со значениями в банаховом пространстве У. Теорема 7. Пусть для некоторой последовательности Tn разбиений Х справедливы соотношения (23) для f1α иf2α и (24) для Fα. Пусть последовательность функций hα удовлетворяет условию в теореме 5, конечномерные распределения (f1α(x, ω), f2α(x, ω)) слабо сходятся к конечномерным распределениям (f1(x, ω), f2(x, ω)), причем для f1и f2 справедливо соотношение (23). Тогда
где L – расстояние Прохорова (см. раздел П-3 приложения 1),
Теорема 7 дает общий метод получения асимптотических распределений статистик интегрального типа. Важно, что соотношение (23) выполнено для эмпирического процесса и для процессов, связанных с оцениванием параметров при проверке согласия [28]. Один из выводов общей теории состоит в том, что в качестве Fα можно использовать практически любую состоятельную оценку истинной функции распределения. Этот вывод использовался при построении критерия типа омега-квадрат для проверки симметрии распределения относительно 0 и обнаружения различий в связанных выборках (см. ниже). Асимптотическое поведение критериев типа Колмогорова может быть получено с помощью описанного выше метода аппроксимации ступенчатыми функциями. Этот метод не требует обращения к теории сходимости вероятностных мер в функциональных пространствах. Для критериев Колмогорова и Смирнова достаточно использовать лишь свойства эмпирического процесса и броуновского моста. В случае проверки согласия добавляется необходимость изучения еще одного случайного процесса. Он является разностью между двумя функциями распределения. Одна - функция распределения элементов выборки. Вторая - случайный элемент параметрического семейства распределений, полученный путем подстановки оценок параметров вместо их истинных значений. Статистика интегрального типа для проверки симметрии распределения. В прикладной статистике часто возникает необходимость проверки гипотезы о симметрии распределения относительно 0. Так, при проверке однородности связанных выборок необходимость проверки этой гипотезы основана на следующем факте [6]. Если случайные величины Х и Y независимы и одинаково распределены, то для функции распределения H(x)=P(Z<x) случайной величины Z = X – Y выполнено, как нетрудно видеть, соотношение H(-x)=1 - H(x). Это соотношение означает симметрию функции распределения относительно 0. Плотность такой функции распределения является четной функцией, ее значения в точках х и (-х) совпадают. Проверка гипотезы однородности связанных выборок в наиболее общем случае сводится к проверке симметрии функции распределения разности Z = X– Y относительно 0. Рассмотрим методы проверки этой гипотезы. Сначала обсудим, какого типа отклонения от гипотезы симметрии можно ожидать при альтернативных гипотезах? Рассмотрим сначала альтернативу сдвига
В этом случае распределение Z при альтернативе отличается сдвигом от симметричного относительно 0. Для проверки гипотезы однородности может быть использован критерий знаковых рангов, разработанный Вилкоксоном (см., например, справочник [34, с.46-53]). Альтернативная гипотеза общего вида записывается как
при некотором х0 . Таким образом, проверке подлежит гипотеза симметрии относительно 0, которую можно переписать в виде H(x) + H(-x) - 1 = 0 . Для построенной по выборке Zj = Xj - Yj , j = 1,2,…,n, эмпирической функции распределения Hn(x) последнее соотношение выполнено лишь приближенно:
Как измерять отличие от 0? По тем же соображениям, что и в предыдущем пункте, целесообразно использовать статистику типа омега-квадрат. Соответствующий критерий был предложен в работе [35]. Он имеет вид
Представим эту статистику в интегральном виде. Рассмотрим выборочный процесс
При справедливости нулевой гипотезы
Положим
Тогда, как легко видеть, статистика, заданная формулой (27), представляется в виде
Таким образом, асимптотическое поведение этой статистики может быть изучено с помощью описанной выше предельной теории статистик интегрального типа. Исторически ход мысли был обратным - сначала была построена и изучена статистика (27), а потом путем обобщения разработанных при анализе конкретной статистики методов исследования была построена общая теория, включающая в себя ряд необходимых и достаточных условий. Критерий проверки гипотезы симметрии распределения относительно 0 с помощью статистики (27) является состоятельным, т.е. если функция распределения элементов выборки не удовлетворяет рассматриваемой гипотезе, то вероятность отклонения гипотезы стремится к 1 при росте объема выборки. В работе [35] найдено предельное распределение этой статистики:
В табл.1 приведены критические значения статистики типа омега-квадрат для проверки симметрии распределения (и тем самым для проверки однородности связанных выборок), соответствующие наиболее распространенным значениям уровней значимости (расчеты проведены Г.В. Мартыновым; см.также [31]). Таблица 1. Критические значения статистики
Как следует из табл.1, правило принятия решений при проверке симметрии распределения (или однородности связанных выборок) в наиболее общей постановке и при уровне значимости 5% формулируется так. Вычислить статистику Пример. Пусть величины Zj , j=1,2,…,20, таковы: 20, 18, (-2), 34, 25, (-17), 24, 42, 16, 26, 13, (-23), 35, 21, 19, 8, 27, 11, (-5), 7. Соответствующий вариационный ряд (-23)<(-17)<(-5)<(-2)<7<8<11<13<16<18< <19<20<21<24<25<26<27<34<35<42. Для расчета значения статистики Таблица 2. Расчет значения статистики
Результаты расчетов (суммирование значений по седьмому столбцу табл.2) показывают, что значение статистики
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
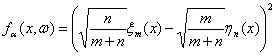 .
.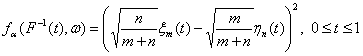 .
.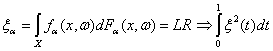 ,
,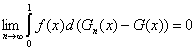 . (4)
. (4)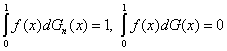
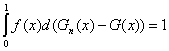 ,
,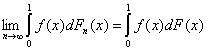 (11)
(11)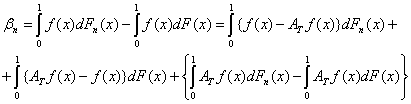 . (15)
. (15)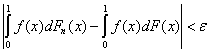 ,
,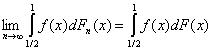 ,
,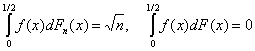 ,
,