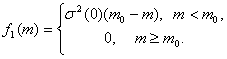«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
М.: МЗ-Пресс, 2004. Глава 2. Статистические методы в пространствах произвольной природы 2.9. Методы шкалирования В прикладной статистике каждый элемент выборки описывается тем или иным математическим объектом, например, нечетким множеством или вектором. Естественным является желание наглядно представить себе имеющиеся статистические данные. Однако человек может непосредственно воспринимать лишь числовые данные или точки на плоскости. Анализировать скопления точек в трехмерном пространстве уже гораздо труднее. Непосредственное (визуальное) восприятие данных более высокой размерности невозможно. Поэтому вполне естественным является желание перейти от многомерной выборки или выборки, состоящей из объектов нечисловой природы, к данным небольшой размерности, чтобы «на них можно было посмотреть». Статистические технологии такого перехода объединяют термином «методы шкалирования». Если исходные данные - многомерные вектора, то говорят о «методах снижения размерности». Кроме стремления к наглядности, есть и другие мотивы для шкалирования и снижения размерности. Те факторы, от которых интересующая исследователя переменная не зависит, лишь мешают статистическому анализу. Во-первых, на сбор информации о них расходуются ресурсы. Во-вторых, как можно доказать, их включение в анализ ухудшает свойства статистических процедур (в частности, увеличивает дисперсию оценок параметров и характеристик распределений). Поэтому желательно избавиться от таких факторов. При анализе данных обычно рассматривают не одну, а множество задач, в частности, по-разному выбирая независимые и зависимые переменные. Поэтому рассмотрим задачу шкалирования (снижения размерности) в следующей формулировке. Дана выборка. Требуется перейти от нее к совокупности векторов малой размерности, максимально сохранив структуру исходных данных, по возможности не теряя информации, содержащейся в данных. Задача конкретизируется в рамках каждого конкретного метода шкалирования (снижения размерности). Метод главных компонент является одним из наиболее часто используемых методов снижения размерности. Основная его идея состоит в последовательном выявлении направлений, в которых данные имеют наибольший разброс. Пусть выборка состоит из n-мерных векторов, одинаково распределенных с вектором X = (x(1), x(2), … , x(n)). Рассмотрим линейные комбинации Y(λ(1), λ(2), …, λ(n)) = λ(1)x(1) + λ(2)x(2) + … + λ(n)x(n), где λ2(1) + λ2(2) + …+ λ2(n) = 1. Здесь вектор λ = (λ(1), λ(2), …, λ(n)) лежит на единичной сфере в n-мерном пространстве. В методе главных компонент прежде всего находят направление максимального разброса, т.е. такое λ, при котором достигает максимума дисперсия случайной величины Y(λ) = Y(λ(1), λ(2), …, λ(n)). Тогда вектор λ задает первую главную компоненту, а величина Y(λ) является проекцией случайного вектора Х на ось первой главной компоненты. Затем, выражаясь терминами линейной алгебры, рассматривают гиперплоскость в n-мерном пространстве, перпендикулярную первой главной компоненте, и проектируют на эту гиперплоскость все элементы выборки. Размерность гиперплоскость на 1 меньше, чем размерность исходного пространства. В рассматриваемой гиперплоскости процедура повторяется. В ней находят направление наибольшего разброса, т.е. вторую главную компоненту. Затем выделяют гиперплоскость, перпендикулярную первым двум главным компонентам. Ее размерность на 2 меньше, чем размерность исходного пространства. Далее – следующая итерация. С точки зрения линейной алгебры речь идет о построении нового базиса в n-мерном пространстве, ортами которого служат главные компоненты. Дисперсия, соответствующая каждой новой главной компоненте, меньше (точнее, не больше), чем для предыдущей. Обычно останавливаются, когда она меньше заданного порога. Если отобрано k главных компонент, то это означает, что от n-мерного пространства удалось перейти к k-мерному, т.е. сократить размерность с n-до k,практически не исказив структуру исходных данных. Для визуального анализа данных часто используют проекции исходных векторов на плоскость первых двух главных компонент. Обычно хорошо видна структура данных, выделяются компактные кластеры объектов и отдельно выделяющиеся элементы выборки. Метод главных компонент является одним из методов факторного анализа [49]. Различные алгоритмы факторного анализа объединены тем, что во всех них происходит переход к новому базису в исходном n-мерном пространстве. Важным является понятие «нагрузка фактора», применяемое для описания роли исходного фактора (переменной) в формировании определенного вектора из нового базиса. Новая идея по сравнению с методом главных компонент состоит в том, что на основе нагрузок происходит разбиение факторов на группы. В одну группу объединяются факторы, имеющие сходное влияние на элементы нового базиса. Затем из каждой группы рекомендуется оставить одного представителя. Иногда вместо выбора представителя расчетным путем формируется новый фактор, являющийся центральным для рассматриваемой группы. Снижение размерности происходит при переходе к системе факторов, являющихся представителями групп. Остальные факторы отбрасываются. Описанная процедура может быть осуществлена не только с помощью факторного анализа. Речь идет о кластер-анализе признаков (факторов, переменных). Для разбиения признаков на группы можно применять различные алгоритмы кластер-анализа. Достаточно ввести расстояние (меру близости, показатель различия) между признаками. Пусть Х и У – два признака. Различие d(X,Y) между ними можно измерять с помощью выборочных коэффициентов корреляции: d1(X,Y) = 1 – rn(X,Y), d2(X,Y) = 1 – ρn(X,Y), где rn(X,Y) – выборочный линейный коэффициент корреляции Пирсона, ρn(X,Y) – выборочный коэффициент ранговой корреляции Спирмена. Процедуры шкалирования. На использовании расстояний (мер близости, показателей различия) d(X,Y) между объектами (или признаками) Х и У основан обширный класс методов многомерного шкалирования [50, 51]. Основная идея этого класса методов состоит в представлении каждого объекта точкой геометрического пространства (обычно размерности 1, 2 или 3), координатами которой служат значения скрытых (латентных) факторов, в совокупности достаточно адекватно описывающих объект. При этом отношения между объектами заменяются отношениями между точками – их представителями. Так, данные о сходстве объектов – расстояниями между точками, данные о превосходстве – взаимным расположением точек [52]. В практике используется ряд различных моделей шкалирования. Во всех них встает проблема оценки истинной размерности факторного пространства. Рассмотрим эту проблему на примере обработки данных о сходстве объектов с помощью т.н. метрического шкалирования. Пусть имеется n объектов О(1), О(2), …, O(n), для каждой пары объектов О(i), O(j) задана мера их сходстваs(i,j). Считаем, что всегда s(i,j) = s(j,i). Происхождение чисел s(i,j) не имеет значения для описания работы алгоритма. Они могли быть получены либо непосредственным измерением, либо с использованием экспертов, либо путем вычисления по совокупности описательных характеристик, либо как-то иначе. В евклидовом пространстве рассматриваемые n объектов должны быть представлены конфигурацией n точек, причем в качестве меры близости точек-представителей выступает евклидово расстояние d(i,j) между соответствующими точками. Степень соответствия между совокупностью объектов и совокупностью представляющих их точек определяется путем сопоставления матриц сходства ||s(i,j)|| и расстояний ||d(i,j)||. Метрический функционал сходства имеет вид
Геометрическую конфигурацию надо выбирать так, чтобы функционал S достигал своего наименьшего значения [52]. Замечание. В неметрическом шкалировании вместо близости самих мер близости и расстояний рассматривается близость упорядочений на множестве мер близости и множестве соответствующих расстояний. Вместо функционала Sиспользуются аналоги ранговых коэффициентов корреляции Спирмена и Кендалла. Другими словами, неметрическое шкалирование исходит из предположения, что меры близости измерены в порядковой шкале. Пусть евклидово пространство имеет размерность m. Рассмотрим минимум среднего квадрата ошибки
где минимум берется по всем возможным конфигурациям n точек в m-мерном евклидовом пространстве. Исходя из общих результатов об асимптотическом поведении решений экстремальных статистических задач (раздел 2.3), можно показать, что в задачах метрического и неметрического шкалирования рассматриваемые минимумы достигаются на некоторых конфигурациях. Ясно, что при росте m величина αm монотонно убывает (точнее, не возрастает). Можно показать, что при m > n– 1 она равна 0 (если s(i,j) – метрика). Для увеличения возможностей содержательной интерпретации желательно действовать в пространстве возможно меньшей размерности. При этом, однако, размерность необходимо выбрать так, чтобы точки представляли объекты без больших искажений. Возникает вопрос: как рационально выбирать размерность, т.е. натуральное число m? В рамках детерминированного анализа данных обоснованного ответа на этот вопрос, видимо, нет. Следовательно, необходимо изучить поведение αm в тех или иных вероятностных моделях. Если меры близости s(i,j) являются случайными величинами, распределение которых зависит от «истинной размерности» m0 (и, возможно, от каких-либо еще параметров), то можно в классическом математико-статистическом стиле ставить задачу оценки m0, искать состоятельные оценки и т.д. Начнем строить вероятностные модели. Примем, что объекты моделируются точками в евклидовом пространстве размерности k, где k достаточно велико. То, что «истинная размерность» равна m0, означает, что все эти точки лежат на гиперплоскости размерности m0. Примем для определенности, что совокупность рассматриваемых точек представляет собой выборку из кругового нормального распределения с дисперсией σ2(0). Это означает, что объектыО(1), О(2), …, O(n) являются независимыми в совокупности случайными векторами, каждый из которых строится как ζ(1)e(1) + ζ(2)e(2) + … + ζ(m0)e(m0), где e(1), e(2), … , e(m0) – ортонормальный базис в подпространстве размерностиm0, в котором лежат рассматриваемые точки, а ζ(1), ζ(2), … , ζ(m0) – независимые в совокупности одномерные нормальные случайные величины с математическим ожиданием ) и дисперсией σ2(0). Рассмотрим две модели получения мер близости s(i,j). В первой из них s(i,j) отличаются от евклидова расстояния между соответствующими точками из-за того, что точки известны с искажениями. Пусть с(1), с(2), … , с(n) – рассматриваемые точки. Тогда s(i,j) = d(c(i) + ε(i), c(j) + ε(j)), i,j = 1, 2, … , n, где d – евклидово расстояние между точками в k-мерном пространстве, вектора ε(1), ε(2), … , ε(n) представляют собой выборку из кругового нормального распределения в k-мерном пространстве с нулевым математическим ожиданием и ковариационной матрицей σ2(1)I, где I – единичная матрица. Другими словами, ε(i) = η(1)e(1) + η(2)e(2) + … + η(k)e(k), где e(1), e(2), …, e(k) – ортонормальный базис в k-мерном пространстве, а {η(i,t), i = 1, 2, … , n, t = 1, 2, … , k} – совокупность независимых в совокупности одномерных случайных величин с нулевым математическим ожиданием и дисперсией σ2(1). Во второй модели искажения наложены непосредственно на сами расстояния: s(i,j) = d(c(i), c(j)) + ε(i,j), i,j = 1, 2, … , n, i ≠ j, где {ε(i,j), i,j = 1, 2, … , n} – независимые в совокупности нормальные случайные величины с математическим ожиданием ) и дисперсией σ2(1). В работе [53] показано, что для обеих сформулированных моделей минимум среднего квадрата ошибки αm приn → ∞ сходится по вероятности к f(m) = f1(m) + σ2(1)(k – m), m = 1, 2, …, k, где
Таким образом, функция f(m) линейна на интервалах (1; m0) и (m0; k), причем на первом интервале она убывает быстрее, чем на втором. Отсюда следует, что статистика
является состоятельной оценкой истинной размерности m0 (сопоставьте с рассмотренными выше оценками истинной размерности модели в задачах восстановления зависимости (раздел 2.7) и расщепления смесей (раздел 2.8)). Итак, из вероятностной теории вытекает рекомендация – в качестве оценки размерности факторного пространства использовать m*. Отметим, что подобная рекомендация была сформулировано как эвристическая одним из основателей многомерного шкалирования Дж. Краскалом [50]. Он исходил из опыта практического использования многомерного шкалирования и вычислительных экспериментов. Вероятностная теория нечисловой статистики позволила обосновать эту давнюю эвристическую рекомендацию. Применение общих результатов нечисловой статистики к методу главных компонент. Напомним, что исходные данные – набор векторов ξ1, ξ2, … , ξn, лежащих в евклидовом пространстве Rk размерности k. Цель состоит в снижении размерности, т.е. в уменьшении числа рассматриваемых показателей. Для этого берут всевозможные линейные ортогональные нормированные центрированные комбинации исходных показателей, получают k новых показателей, из них берут первые m, где m < k (подробности см. выше). Матрицу преобразования С выбирают так, чтобы максимизировать информационный функционал
где x(i), i = 1, 2, … , k, - исходные показатели; исходные данные имеют вид ξj = (xj(1), xj(2), … , xj(k)), j = 1, 2, … , n; при этом z(α), α = 1, 2, … , m, - комбинации исходных показателей, полученные с помощью матрицы С. Наконец,s2(z(α)), α = 1, 2, … , m, s2(x(i)), i = 1, 2, … , k, - выборочные дисперсии переменных, указанных в скобках. Укажем подробнее, как новые показатели (главные компоненты) z(α) строятся по исходным показателям x(i) с помощью матрицы С:
где
Матрица C = ||cαβ|| порядка mЧk такова, что
(нормированность),
(ортогональность). Решением основной задачи метода главных компонент является
где минимизируемая функция определена формулой (1), а минимизация проводится по всем матрицам С, удовлетворяющим условиям (2) и (3). Вычисление матрицы Сn – задача детерминированного анализа данных. Однако, как и в иных случаях, например, для медианы Кемени, возникает вопрос об асимптотическом поведении Сn. Является ли решение основной задачи метода главных компонент устойчивым, т.е. существует ли предел Сn при n → ∞? Чему равен этот предел? Ответ, как обычно, может быть дан только в вероятностной теории. Пусть ξ1, ξ2, … , ξn - независимые одинаково распределенные случайные вектора. Положим
где матрица C = ||cαβ|| удовлетворяет условиям (6) и (7). Введем функцию от матрицы
Легко видеть, что при n → ∞ и любом С
Рассмотрим решение предельной экстремальной задачи
Естественно ожидать, что
Действительно, это соотношение вытекает из приведенных выше общих результатов об асимптотическом поведении решений экстремальных статистических задач. Таким образом, теория, развитая для пространств произвольной природы, позволяет единообразным образом изучать конкретные процедуры прикладной статистики.
|
||