«Управление и Оптимизация Производственного Предприятия»
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Анализ устойчивости относительно поставленной цели как один из подходов к описанию функционирования организации в условиях неопределенности Монография, Самара, 2001. Глава 6. Задачи оптимизации по критерию устойчивости относительно поставленной цели В данной части исследования будут исследованы возможности управления устойчивостью путем изменения параметров стратегического и тактического целеуказаний. Как было показано в главе 2, общая модель целеуказания имеет вид:
где Постановка задач Общая постановка задачи
То есть при заданных ограничениях, накладываемых на параметры целеуказания, необходимо подобрать такие их значения, при которых устойчивость относительно поставленной цели максимальна. Как видно, такого рода задачи можно ставить и решать как в случае функционирования организации по неизменной программе, так и для любой модели «включенного» текущего управления: ЗЛП, транспортной задачи, задачи минимизации риска инвестирования и др. Кроме того, можно поставить специальные задачи максимизации устойчивости. При постановке задачи Несмотря на довольно узкий круг возможностей эффективного 1. Задача обслуживания кредиторской задолженности организации и сопряженные с ней варианты и разновидности, относящиеся к задачам управления устойчивостью относительно поставленной цели при неизменной программе функционирования организации. 2. Задача управления производством продукции в условиях неопределенности при «включенном» текущем управлении (с использованием модели линейного программирования, приведенной в главе 5). На наш взгляд, наибольший интерес представляет возможность управления графиком обслуживания задолженности предприятия, и особенно задолженности по полученному кредиту, так как по данному параметру меньше всего ограничений: если кредит коммерческий, то его выплату можно растянуть довольно надолго – главное проценты платить, а если кредит льготный, то можно поставить ограничение на срок и сумму выплат и в течении этого срока платить, как удобно. Так же можно поступать и с кредиторской задолженностью, установив пени за просроченные выплаты. В этой связи поставим и решим задачу оптимального по устойчивости управления финансированием реализации сложных проектов. При управлении реализацией крупных и средней величины проектов принято разбивать их на стадии, этапы, упорядоченные во времени. Каждый этап проекта имеет свою продолжительность, результат и стоимость реализации. При этом возможны самые разнообразные схемы финансирования реализации этапов: за счет получения кредитов, за счет доходов, полученных от реализации предыдущих этапов, комбинированные способы. Допустимыми из них являются только те, которые обеспечивают своевременное и полное финансирование реализации этапов. В современных условиях получение кредитных средств весьма проблематично и дорогостояще, поэтому часто приходится конструировать такие схемы, при которых кредит берется однажды, на первом этапе реализации проекта, а финансирование последующих этапов происходит за счет доходов, полученных на предыдущих этапов. Такие схемы рефинансирования, как правило, менее выгодны с точки зрения интегральных результатов реализации проекта, менее надежны, а также увеличивают срок реализации проекта, но зачастую являются самым доступным, если не единственным, решением проблемы финансирования проекта, учитывая ограничения на объем кредитных средств. Приведем несколько примеров подобных ситуаций. 1. Для реализации инвестиционного проекта предприятию необходимо взять кредит. Но залог, необходимый для получения требуемой суммы, отсутствует. Поэтому кредит берется не в полном объеме, а в соответствии с тем залогом, который имеется, а остальные средства планируется рефинансировать, разбив проект на несколько этапов. Разновидностью данной ситуации является ситуация, когда есть возможность получить два кредита: один льготный, но его сумма ограничена, другой на общих основаниях, но такой дорогой, что резко понижает эффективность проекта. Поэтому берется льготный кредит, а остальные средства рефинансируются. 2. На предприятии разработана программа выхода из кризиса, которая предусматривает финансирование определенных мероприятий. Для получения коммерческого кредита, необходимого для полного восстановления производства, предприятие недостаточно платежеспособно. Но есть возможность получить, например, налоговый кредит, что и делается, в результате чего предприятие постепенно выходит на программную мощность, финансируя развитие за счет текущих доходов. 3. Разработан план комплексного инвестирования экономики региона. Для этого выделено несколько ключевых предприятий, оценены их социально-экономическая значимость, инвестиционная емкость, эффективность инвестиций, в результате чего разработан план инвестирования, в соответствии с которым финансирование идет в несколько этапов, и на каждом этапе кредиты получает определенное количество предприятий, причем кредитные средства, инвестируемые на каждом последующем этапе, – это доходы от деятельности ранее прокредитованных предприятий, отвлеченные от них на основе участия инвестора в акционерном капитале предприятия, договоров об инвестировании, налоговых сборов и т.п. 4. В рамках действующего предприятия реализуется инвестиционный проект. Экономическое положение предприятия бедственное, так как основное производство неэффективно. Поэтому для покрытия текущих убытков и для получения средств на реструктуризацию производства необходим приток денежных средств в определенных размерах, единственным источником которого является успешно развивающийся проект. Возможны и другие ситуации, но общей для объектов исследования чертой является целеполагание: обеспечить реализацию проекта в установленные сроки, из чего следует целеуказание: в i-м отчетном периоде необходимо иметь не менее Итак, пусть организация в i-м периоде функционирования имеет доход Для учета дисконтирования при распределении сумм выплат рассмотрим графическую иллюстрацию процесса погашения кредита. Пусть Р – величина взятого кредита на начало периода планирования, n – число отчетных периодов, r – коэффициент возрастания суммы выплат за i-й период. Если выплаты производятся в конце периода, то процесс погашения кредита иллюстрируется следующим образом:
Числами 1,2,..., n обозначены номера периодов, ниже указаны, соответственно, суммы выплат кредита в каждом периоде и остаток на конец периода. Отсюда видно, что кредит будет погашен полностью за рассматриваемый отрезок времени при выполнении условия
Если требование задачи таково, что в i-м периоде необходимо иметь не менее
а устойчивость относительно поставленной цели рассчитывается по формуле: где Устойчивость относительно поставленной цели за период планирования, таким образом, составляет Для решения задачи используем метод условной оптимизации Лагранжа. В соответствии с данным методом, выполняется преобразование целевой функции:
Приравняв к нулю частные производные F по
Полученное решение для Другие условия, например, продиктованные банком, также можно занести в оптимизационную модель, при этом решение будет чуть сложнее формализовать. Как видно, решение данной задачи сопряжено с определенными трудностями технического характера. Современные ЭВМ не всегда способны обеспечить ее решение за приемлемый срок и с приемлемой точностью, часты отказы. Поэтому в ряде случаев необходимо упростить вид и структуру уравнений системы, что можно сделать лишь путем подбора функции плотности распределения. Наиболее удачный вариант – нормальное распределение. Конечно, с точки зрения теории оно слабо подходит для описания вариаций параметров доходов и переменных издержек, но та погрешность, которая имеет место вследствие допущения нормальности распределения данных параметров, несущественным образом отражается на полученном решении. Приведем пример. Для реализации инвестиционного проекта необходимы инвестиции в размере 852 тыс. руб., но объем доступных кредитных средств ограничен величиной в 250 тыс. руб. Поэтому для обеспечения полной реализации проекта составлен следующий календарный план (Т а б л и ц а 6.1). Т а б л и ц а 6.1 Календарный план реализации инвестиционного проекта
Примечание: стоимости этапов 1,2 компенсируются из собственных средств учредителей. Кредит берется однажды, под льготный процент – 15% годовых (4,78% в отчетный период), в размере 250 тыс. руб. и сроком на год. Дата получения кредита – 01.09.2001 г. Требуется составить график выплат тела кредита и процентов по кварталам, по которому вероятность выполнения календарного плана была бы максимальна. В Т а б л и ц е 6.2 приведен график денежных потоков в течении периода с 01.09. 2001г. по 01.09. 2002 г. с разбивкой по отчетным периодам. Т а б л и ц а 6.2 Движение денежных средств в рамках инвестиционного проекта
Примечание: в расчетах никак не учитывается налог на прибыль, потому что, согласно закону РФ «О налоге на прибыль предприятий и организаций», та часть выручки от реализации за вычетом всех издержек, которая направляется на расширение и модернизацию производства, налогом на прибыль не облагается. Экспертным путем установлено, что с вероятностью 90% параметры: поступления от продаж и переменные затраты варьируют в определенных интервалах, границы которых приведены в нижеследующей таблице. Примем, что данные показатели имеют нормальное распределение. Среднеквадратические отклонения их величин также приведены в Т а б л и ц е 6.3. Т а б л и ц а 6.3 Параметры распределений характеристик проекта
Решение задачи в виде вектора
Здесь
Предположим, что предприятие имеет возможность не только брать кредит единожды, но и совершать другие финансово-кредитные операции: брать другие кредиты и инвестировать или депонировать свободные денежные средства. Тогда ограничение неотрицательности на m не накладывается и, как следствие, открываются дополнительные возможности увеличения устойчивости. Можно, например, запланировать взятие краткосрочного кредита на периоде, где предстоят особенно большие инвестиционные расходы, или вложить в банк определенную сумму денег в относительно «благополучном», по предварительным расчетам, периоде, и востребовать ее в будущих периодах, а также осуществлять другие допустимые финансовые операции. Для математической формализации данных операций введем следующие обозначения:
устойчивость относительно поставленной цели рассчитывается по формуле:
В этом случае поставленная задача решается аналогично, а возрастание возможностей предприятия по оптимизации финансово-кредитной деятельности учитывается путем введения новых переменных –
Группы ограничений (1) и (2) нуждаются в пояснении их смысла. Группа ограничений (1) описывает движение кредитов. А кредит сначала берут, а потом отдают, из чего следует ограничение На практике данная система ограничений может быть дополнена ограничениями неотрицательности, накладываемыми на некоторые из Вернемся к нашему примеру. Введем вторую (запасную) кредитную линию,
При этом устойчивость относительно поставленной цели составляет 39,1%, причем минимальная устойчивость (9-12.2000 г.) составляет 68,5%, что несколько ниже соответствующего показателя, полученного ранее, без учета возможности получения дополнительного кредита и депонирования свободных денежных средств. Однако данное решение более предпочтительно, чем полученное ранее, по двум причинам: во-первых, в данном случае устойчивость относительно поставленной цели в целом за период планирования существенно выше; во-вторых, относительно малая устойчивость исследуемой организации в периоде 9-12.2000 г. реально увеличивается за счет «аппаратной избыточности»: дело в том, что при целеуказании геометрическое место точек изображающей области цели бралось выше требуемого критического уровня, поэтому неучтенные при анализе устойчивости свободные денежные средства, каким-либо образом накапливаясь (на том же депоненте), могут создать реальный, но формально не учитываемый запас устойчивости в заключительном интервале периода планирования. Заметим также, что несмотря на сильную разницу в ставках процента по льготному и коммерческому кредитам последний является в данном примере значительно более мощным средством повышения устойчивости, чем депонент, что подтверждается результатами решения нашей задачи без учета возможности депонирования свободных денежных средств:
устойчивость относительно поставленной цели при котором составляет 39,3%, что даже больше, чем при осуществлении операций с депонированием. Причем увеличение ставки по депоненту, если учитывать эту возможность, очень слабо влияет на устойчивость: так, при возрастании ставки до 45% годовых, устойчивость практически не меняется. Слабое влияние на устойчивость относительно поставленной цели оказывает и изменение ограничений на сумму кредита и на объемы операций по депонированию: так, с увеличением допустимых сумм коммерческого кредита с 400 тыс. руб. до 800 тыс. руб. в квартал устойчивость относительно поставленной цели не изменяется (видимо, из-за того, что кредит дорогой), а с уменьшением допустимых сумм до 200 тыс. руб. в квартал устойчивость уменьшается на сотые доли процента; с увеличением и снижением лимита операций по депонированию с 50% до 80% и с 50% до 25% от величины чистой прибыли без учета налогов показатель устойчивости практически не меняется, потому что, как видно из основного решения, объем операций по депоненту невелик. Таким образом, возможности использования коммерческого кредита сильно сужены из-за его дороговизны, а депонирование свободных денежных средств является в данном примере скорее необходимой технической операцией, применяемой для «сбрасывания» свободных денежных средств в ходе реализации проекта, а не эффективным инструментом управления устойчивостью. Рассмотрим проблему с позиций акционера или инвестора, тем более, что его доход (дивиденды или какие-либо фиксированные выплаты) также является параметром целеуказания. С одной стороны, акционер заинтересован в устойчивом функционировании проекта, но с другой стороны он стремится максимизировать свой доход от его реализации в виде дивидендов. Так же и менеджеры проекта: с одной стороны, если каждый участник проекта не получит удовлетворяющий его бонус, проект не состоится, но, с другой стороны, любое отвлечение доходов может затруднить его реализацию. Таким образом, формальная модель принятия решения, если учитывать интересы акционеров или инвесторов, содержит как минимум два критерия: максимум устойчивости относительно поставленной цели (реализация проекта в установленные сроки) и максимум доходности по акциям*, причем неплохо бы выплачивать дивиденды как можно раньше с начала реализации проекта. При этом необходимо расплатиться с кредитом. Возникает задача: найти такое сочетание устойчивости и доходности, которое бы удовлетворяла интересам акционеров и менеджеров проекта. Очевидно, оптимумы целевых функций менеджеров и акционеров далеки друг от друга по структуре решения, однако существует компромиссное решение, которое получается путем ввода новой, синтетической целевой функции, отражающей требование максимума устойчивости и максимума доходности по акциям в определенных пропорциях. Подчеркнем, что синтетическая целевая функция – это формальное описание механизма согласования интересов двух сторон, имеющих нетождественные интересы: менеджеров проекта и акционеров. Она дает основу для оптимизации процесса согласования этих интересов, в том смысле что при условии адекватности описания данной функцией соотношения интересов ее максимум иллюстрирует оптимальное их сочетание. Мерой адекватности синтетической целевой функции реальному механизму согласования интересов является приемлемость полученного с ее помощью решения как для менеджеров проекта, так и для акционеров. Выделим три варианта ее конструирования: 1. В виде линейной или нелинейной комбинации целевых функций максимума устойчивости и максимума доходности по акциям. 2. В виде целевой функции максимума доходности по акциям, при этом устойчивость фиксируется на определенном уровне и вводится в ограничения модели. 3. В виде целевой функции максимума устойчивости при фиксированной величине доходности по акциям. Отметим, что поставленную задачу нельзя решить, пользуясь специальными методами решения многокритериальных задач, потому что и целевые функции, и ограничения нелинейны. Пусть дивиденды за некоторый период составляют
и формулу устойчивости в i-м периоде:
Тогда задача в формальной постановке имеет вид:
где d – ставка дисконтирования. Задача может быть дополнена выведенными выше ограничениями, если существуют дополнительные кредитные линии и (или) осуществляется депонирование свободных денежных средств, или ограничением неотрицательности для Рассмотрим первый вариант. Его применение в случае линейной комбинации целевых функций может быть результатом последовательных согласований интересов менеджеров по управлению проектом и акционерами, что выражается в присвоении критериям устойчивости и доходности по акциям определенных весов, отражающих их сравнительную значимость. В этом случае управляющие проектом менеджеры заинтересованы в преобладании критерия устойчивости над критерием доходности по акциям, поскольку выплаты дивидендов означают отвлечение средств от финансирования этапов реализации проекта и как следствие сильную головную боль менеджерам, т.к. в этом случае приходится прилагать больше усилий на обеспечение необходимого сальдо денежных потоков и вообще свободных денег будет мало. Акционеры, в свою очередь, по понятным причинам больше заинтересованы в получении дохода. С другой стороны, и у менеджеров, и у акционеров есть заинтересованность в максимизации критериев, отражающих противоположные интересы: без привлечения средств акционеров реализация проекта не состоится, а без обеспечения необходимой устойчивости получить хорошие дивиденды невозможно. Поэтому существует некая область согласования интересов менеджеров и акционеров, и, значит, оптимальное решение исходной двухкритериальной задачи эквивалентно решению однокритериальной задачи с синтетической целевой функцией, если веса критериев принадлежат области согласования интересов менеджеров и акционеров. Итак, пусть критериям устойчивости и доходности по акциям приданы веса
Последнее ограничение означает, что сумма выплаченных дивидендов в i-м периоде не может превосходить по величине определенного лимита, иначе их выплатить заведомо невозможно. Лимитом может быть, например, определенная доля чистой прибыли. В данном случае при решении задачи удобнее пользоваться не методом условного экстремума Лагранжа, как в задаче распределения сумм выплат кредита, а методами численной оптимизации (например, градиентными методами), поэтому результата решения для Применение нелинейных комбинаций критериев доходности по акциям и устойчивости дает следующие возможности: 1. Позволяет более тесно связывать требования устойчивости и доходности, чем наблюдается при линейной комбинации критериев. 2. Позволяет конструировать механизм согласования интересов менеджеров проекта и акционеров, более адекватный реальному, чем взвешенная сумма соответствующих критериев. 3. Представление целевой функции в виде нелинейной комбинации позволяет управлять устойчивостью и доходностью при любых значениях параметров комбинации, чего не наблюдается в случае линейной комбинации, где оптимальное решение получается лишь в том случае, если веса принадлежат области согласования интересов менеджеров проекта и акционеров; следовательно, использование нелинейных комбинаций дает бо¢льшую возможность получить решение, устраивающее как акционеров, так и менеджеров проекта, чем применение взвешенной суммы критериев. Обозначив критерии устойчивости и доходности соответственно через R и A, выделим среди нелинейных комбинаций критериев следующие: 1. Произведение критериев устойчивости (R) доходности по акциям (А). Эту целевую функцию нельзя считать математическим ожиданием доходности по акциям, так как величина выплачиваемых дивидендов в определенном периоде может напрямую не зависеть от нарушения сроков реализации определенных этапов проекта, однако она дает наглядное представление о взаимосвязи критериев устойчивости и доходности по акциям: чем выше устойчивость, тем меньше нужно платить дивидендов, и наоборот. 2. Целевая функция вида Использование этой целевой функции позволяет при управлении устойчивостью и доходностью придавать большее (меньшее) значение тому или иному критерию путем увеличения (уменьшения) соответствующего показателя степени, что позволяет корректировать результат, полученный при применении критерия R·A, т.е. «подогнать» результат таким образом, чтобы он был наиболее предпочтителен для менеджера проекта и все еще устраивал акционеров. 3. Целевая функция вида
учитывающая взаимосвязь критериев устойчивости и доходности и содержащая определенное структурное ограничение на рост А, и предоставляющая массу возможностей для корректировки результата решения задачи путем изменения значений параметров Можно вывести еще ряд синтетических целевых функций нелинейного вида, пользуясь одним правилом: конструировать целевую функцию так, чтобы ни при каком значении параметра, входящего в нее, интересы одной стороны не доминировали над интересами другой в абсолютной степени* . Вне зависимости от выбора синтетической целевой функции, т.е. способа формального описания согласования интересов менеджеров проекта и акционеров, сохраняются общие для оптимизационной модели ограничения на суммы выплат дивидендов и возврат кредита в полном объеме в определенный срок. При любом виде целевой функции задача решается методами численной оптимизации. Рассмотрим второй вариант конструирования синтетической целевой функции, при котором устойчивость фиксируется на определенном уровне и заносится в ограничения задачи, а целевой функцией является доходность по акциям. Это вариант применяется в ситуации, когда менеджеры проекта принимают решение: если устойчивость относительно поставленной цели с учетом выплат дивидендов окажется меньше определенного уровня, реализовывать этот проект им не стоит – слишком велик риск невыполнения календарного плана. Тогда, определившись с критическим значением устойчивости, менеджер получает наиболее выгодный для акционеров план выплаты дивидендов при фиксированной устойчивости. Оптимизационная модель в этом случае имеет вид:
Как видно, ограничения по суммам выплат дивидендов отсутствуют: если менеджеры выбрали для себя критическое значений устойчивости относительно поставленной цели, достать необходимые средства для выплаты дивидендов – их проблема, зато система ограничений может быть дополнена ограничениями на суммы выплат процентов и дивидендов в некоторых периодах, если эти условия наложены банком или акционерами. Заметим, что в данном случае ограничение
Третий вариант конструирования целевой функции, когда максимизируется устойчивость при фиксированной величине дивидендов, применяется в случаях, когда акционеры диктуют минимальный уровень доходности, который их интересует, а менеджеры проекта, исходя из требований акционеров, максимизируют устойчивость относительно поставленной цели. Отсюда оптимизационная модель имеет вид:
В данном случае, как и во втором варианте, ограничение
Заметим, что три предложенных варианта отражают последовательные стадии процесса согласования интересов акционеров и менеджеров проекта. Менеджеры проекта всегда владеют бо¢льшим количеством информации о проекте, чем акционеры, поэтому им принадлежит право первого хода в этой игре, а раз так, то любой вариант продиктован в первую очередь интересами менеджеров, а согласие с акционерами достигается путем балансирования доходов по акциям и устойчивости. Процесс согласования начинается с первого варианта, который предоставляет огромное количество возможных комбинаций устойчивости и доходности по акциям (благодаря различным способам задания вида целевой функции и ее параметров). Если по первому варианту не достигается согласия, менеджеры проекта переходят ко второму варианту, последовательно выбирая приемлемые для себя «критические» значения устойчивости – от больших до предельно низких, в надежде получить «отмашку» от акционеров на наиболее приемлемый для себя вариант. Если же второй вариант не дает компромиссного решения, т.е. желаемая акционерами доходность по акциям не выяснена, она выясняется, и согласование происходит исходя из нее, т.е. работает третий вариант. Если решение по третьему варианту дает столь малую устойчивость, что менеджеры не считают реализацию проекта целесообразной, очередь уступать за акционерами. Из сказанного видно, что в процессе согласования интересов акционеров и менеджеров проекта согласие наступает либо сразу же, либо и те, и другие, как бы торгуясь, постепенно сдают свои позиции, доходя до некоторого предельно приемлемого уровня, после которого реализация проекта слишком рискованна, с точки зрения хотя бы одной из сторон. Процесс поиска компромиссного решения можно проиллюстрировать схемой, изображенной на рисунке 6.1. Математически процесс согласования иллюстрируется функцией устойчивости от доходности по акциям. Аргументом данной функции является дисконтированная сумма выплат дивидендов по периодам, а функцией – устойчивость, рассчитанная при оптимальном распределении выплат данной суммы, т.е.
Р и с. 6.1. Процесс поиска компромиссного решения.
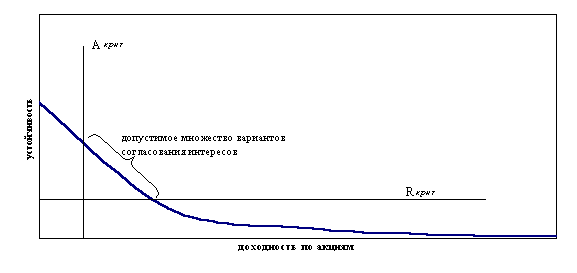
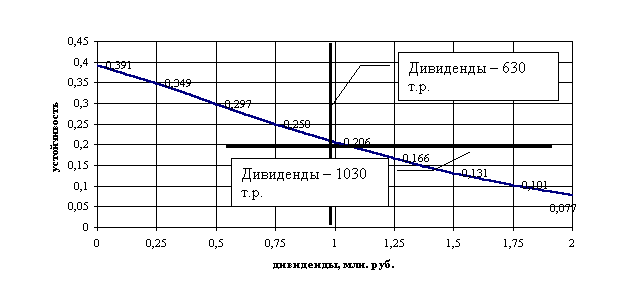
Р и с. 6.2. Зависимость устойчивости от дивидендов. Параметры кривой уточняются в каждом конкретном случае. И акционеры, и менеджеры имеют минимальный уровень притязаний по соответствующему критерию, что отражается путем установления ограничений на область изменения параметров устойчивости и доходности (перпендикулярные абсциссе и ординате прямые). Таким образом, участок графика функции устойчивости от доходности по акциям, лежащий между точками А и R, есть допустимое с точки зрения минимальных интересов менеджеров и акционеров множество вариантов согласования интересов, где каждому выбранному значению доходности по акциям соответствует единственное оптимальное значение устойчивости, и наоборот. Различные стадии процесса поиска компромиссного решения соответствуют различным участкам на графике. Так, случаю когда и менеджеры, и акционеры соглашаются на первой стадии процесса соответствует участок на графике между горизонтальной и вертикальной линиями, не включая крайние точки. Случаю когда, не получив согласия акционеров на предложенный на первой стадии вариант, менеджеры предлагают акционерам вариант, соответствующий минимально приемлемому уровню устойчивости и последние соглашаются, соответствует точка R; случаю когда акционеры, не достигнув согласия с менеджерами на второй стадии, называют минимально приемлемую сумму дивидендов и менеджеры соглашаются, соответствует точка А. Допустимое множество строится с целью выяснить существование компромиссных вариантов, т.е. для проверки возможности решения задачи при имеющихся исходных данных. При отсутствии непустого допустимого множества принимается одно из двух решений: либо прекратить процесс согласования интересов и, следовательно, реализацию проекта, либо корректировать интересы по предложенной схеме. Чем больше расстояние между точками R и А, тем более вероятно, что согласие будет достигнуто на первой стадии процесса, тем больше возможностей именно для согласования интересов обеих сторон, а не для диктата интересов одной стороны, хотя следует отметить, что согласие на первой стадии представляется маловероятным даже при довольно мощном допустимом множестве. Рассмотрим возможный ход процесса согласования в приведенном выше примере. Параметры ситуации возьмем произвольно. Пусть в проекте участвуют несколько акционеров, которые вкладывают в проект активы (производственное помещение, технологии, обеспечивают сбыт, поддержку проекта территориальной администрацией) в определенной пропорции, оцененные в 2,1 млн. руб. Все остальные параметры задачи остаются без изменений: доступна вторая кредитная линия и осуществляется депонирование свободных средств. Для простоты рассуждений предположим, что дивиденды выплачиваются пропорционально величине вклада акционера, иные ситуации не оказывают принципиального влияния на решение задачи. По данному примеру построен график функции устойчивости от общей величины запрашиваемых акционерами дивидендов* (Р и с. 6.3).
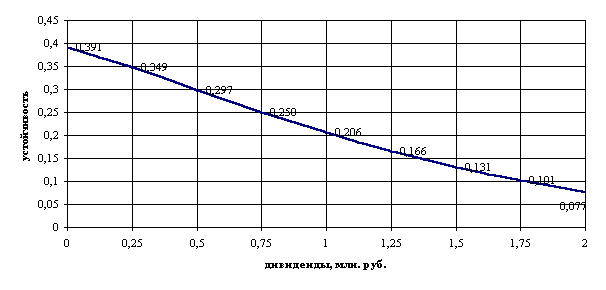
Р и с. 6.3. Зависимость устойчивости относительно поставленной цели от суммы выплат дивидендов. Для определения допустимого множества вариантов зададим его границы. Пусть менеджеры считают приемлемым выполнение проекта при значении устойчивости не менее 0,2, или, в среднем, 0,67 за рассчетный период. Это соответствует максимально возможной величине получаемых дивидендов примерно в 1,03 млн. руб., что эквивалентно сумме в 257,5 тыс. руб. в отчетный период, с учетом принятой ставки дисконтирования. Исходя из тактических соображений, менеджеры в ходе предварительных переговоров с акционерами должны оперировать суммой обещаемых дивидендов, значительно меньшей рассчитанной. Акционеры, в свою очередь, желают оправдать вложенные в дело активы по крайней мере на 30% в течение рассматриваемого периода, т.е. их интересует сумма дивидендов не менее 630 тыс. руб., или 157,5 тыс. руб. в отчетный период. Эта сумма дивидендов соответствует значению устойчивости в 0,274, или, в среднем 0,724 за расчетный период. Следует полагать, что акционеры потребуют большую сумму дивидендов, чем эта, поскольку 630 тыс. руб. – это наименьшая сумма, при которой исполнение проекта представляется акционерам целесообразным. Итак, допустимое множество альтернатив представляет собой участок на нижеследующем графике (Р и с. 6.4), ограниченный вертикальной и горизонтальной линиями.
Р и с. 6.4. Допустимое множество альтернатив. Из графика видно, что допустимое множество достаточно мощно, т.е. у акционеров и менеджеров существует много возможностей сойтись на приемлемых друг для друга вариантах. По крайней мере, если согласие не наступит уже на первой стадии, есть много возможностей для взаимных уступок. В заключении сделаем следующие замечания. Процесс согласования интересов менеджеров и акционеров промоделирован исходя из концепции устойчивости относительно поставленной цели. На практике движущей силой этого процесса является не повышение этой самой устойчивости, а, например, большая свобода и легкость принятия управленческих решений, возникающая как следствие достаточно весомого бюджета, доступного менеджерам проекта. Каждый проект-менеджер хочет иметь как можно больше финансовых средств под рукой, но, наверное, ничтожная часть этих менеджеров в курсе рассматриваемой в данной работе теории и, тем более, связи между величиной свободных денег на счетах организации и ее устойчивостью в предложенном понимании. Менеджерам совершенно необязательно мотивировать свои действия повышением этой самой устойчивости; просто устойчивость, как представляется, может быть индикатором определенных явлений, возникающих в ходе функционирования широкого класса экономических систем. Что касается различий между выплатами дивидендов и интегральными показателями эффективности инвестиций, рассчитываемыми в любом бизнес-плане по официально установленной методике, например, чистой дисконтированной стоимостью (NPV), то последний лишь указывает на эффективность проекта, а вовсе не представляет собой мешочек с деньгами, складывающийся после некоторого расчетного срока. Формой проявления чистой дисконтированной стоимости являются суммы выплат держателям проекта со счетов, относящихся к реализуемому проекту, которые можно трактовать в том числе и как дивиденды. Поэтому в данной главе интегральные показатели эффективности инвестиций не применялись. При «включенном» текущем управлении структура 1. Пусть при управлении ассортиментом и структурой производства продукции в зависимости от удельной прибыльности каждого ее вида используется оптимизационная модель линейного программирования. Как было показано в главе 5, в зависимости от параметров удельной прибыльности задача имеет несколько оптимальных решений, при каждом из которых устойчивость относительно поставленной цели различна. Пусть на момент принятия решения было выбрано базовое решение, оптимальное без учета возможных вариаций параметров удельной прибыльности. Для выполнения заданной производственной программы было закуплено необходимое количество сырья, настроены определенные производственные мощности, осуществлены другие подготовительные меры. Но ситуация с удельной прибыльностью изменилась, и оптимальным становится другой план выпуска, для которого нужно другое сырье, другие производственные мощности и т.п., что обеспечивается не мгновенно. В этом случае было бы резонно выбрать такое решение, при котором устойчивость относительно поставленной цели максимальна. 2. Фирма размещает заказы на своих предприятиях с различной себестоимостью производства. Так как предприятия принадлежат фирме, то она покрывает реальные расходы на производство, а не ту сумму, которая значилась бы в договорах, будь предприятия самостоятельны. План размещения заказов, имеющий минимальную суммарную себестоимость, составляется с применением алгоритма транспортной задачи. В соответствии с оптимальным планом, составленным без учета неопределенности параметров удельной себестоимости изготовления заказов, заказ размещается в определенных пропорциях на определенных предприятиях. Но вот, заказ выполнен, а по счетам, представленным за изготовление продукции, фактическая себестоимость отличается от плановой, так что выгоднее было бы размещать заказ по другому плану. Остается только сожалеть, хотя можно было бы, определив целеуказание относительно себестоимости, составить план, имеющий максимальную устойчивость относительно поставленной цели. 3. На конкурс по размещению кредитных средств региональной администрации представлен ряд инвестиционных проектов. Объем кредитных средств ограничен, поэтому приходится выбирать проекты, руководствуясь определенным критерием. С другой стороны, имеется ряд социально-экономических проблем, которые в определенной мере сможет решить реализация проектов, как-то: обеспечить налоговые поступления, открыть новые рабочие места, обеспечить необходимый уровень промышленного производства и прочее. Как выбирать? Не отрицая всех существующих на сегодняшний день формальных и неформальных критериев отбора, в работе предлагается критерий, имеющий в основе устойчивость относительно поставленной цели, которую имеет каждый из представленных на конкурс проект. Применение метода анализа устойчивости в задачах Множество стратегий развития системы, возможно приводящих систему к достижению поставленной цели, может быть как счетным (дискретным), так и несчетным (непрерывным). Если множество возможных стратегий счетно, то поставленная задача решается элементарно: из множества стратегий выбирается та, при которой поставленная цель достигается с наибольшей вероятностью. Если множество возможных стратегий несчетно, или счетное множество возможных стратегий очень велико, то параметры оптимальной по критерию устойчивости стратегии находятся путем максимизации функции вероятности достижения цели от параметров функционирования системы, любое сочетание которых, как было оговорено, определяет некоторую стратегию, при ограничениях, отражающих специфику конкретной ситуации. В качестве примера задачи определения оптимальной стратегии из несчетного множества возможных приведем задачу оптимизации производственного плана на предприятии в отчетном периоде при ограниченных ресурсах. Пусть предприятие производит продукцию n видов, причем удельная прибыльность i-того вида продукции составляет
Здесь Если при решении учитывать расход сырья на выполнение программы, излишек сырья (или ресурсов), стоимость хранения или утилизации сырья или упущенную выгоду от его неиспользования, то возникает первая подзадача основной задачи максимизации устойчивости при линейной оптимизационной модели, целевая функция которой примет вид
где k – число видов сырья, вызывающих дополнительные расходы от его недоиспользования, Можно поставить вторую подзадачу – увеличить запас имеющихся ресурсов (особенно дефицитных) на
Если плата за дополнительное количество некоторого ресурса взимается как доля от объема продаж, из
Всякий раз, когда имеет место, с одной стороны, довольно большие количества недоиспользованных ресурсов, а с другой стороны – дефицитные ресурсы, нехватка которых здорово снижает эффективность производства, возникает задача: выбрать такие количества привлекаемых сверх лимита ресурсов,
и к управляемым параметрам Решим поставленные задачи на конкретном примере. Пусть на предприятии в ближайшем отчетном периоде планируется производство четырех видов продукции: 1,2,3,4. В результате финансовых расчетов установлено, что в течение года реализация единицы продукции определенного вида принесет некоторую прибыль, значения которой распределены по нормальному закону в некотором доверительном интервале, составленным с надежностью 0,9. В то же время, есть ограничения на объем имеющихся ресурсов, производственную мощность и емкость сегмента рынка, на котором планирует функционировать предприятие. Численные данные приведены в нижеследующих Т а б л и ц а х 6.4, 6.5 (данные приведены за месяц). Цель функционирования предприятия задана величиной прибыли, большей или равной 15000 руб. в месяц. Требуется определить, наиболее устойчивую к случайным отклонениям удельной прибыльности стратегию достижения поставленной цели. Т а б л и ц а 6.4 Исходные данные (1)
Обозначения: I – товар, II – объем производства, единиц, III – прибыль от реализации единицы товара (удельная прибыльность), руб./ед., IV – доверительный интервал для удельной прибыльности, V – расход сырья 1-го вида на изготовление единицы товара (усл. ед.), VI – расход сырья 2-го вида на изготовление единицы товара, VII – расход рабочей силы на изготовление единицы товара (чел.-час.), VIII – расход оборудования на единицу товара (машино-часов). Т а б л и ц а 6.5 Исходные данные (2)
Вначале определим среднеквадратичные отклонения величин удельной прибыльности каждого товара из уравнения:
где Устойчивость функционирования предприятия как функцию от стратегии, на основании общей формулы устойчивости, определим как линейную свертку нормальных законов распределения независимых случайных величин:
Тогда математическая модель задачи примет вид:
Решая данную задачу при помощи пакета «Поиск решения» электронной таблицы Microsoft Excel, получаем, что наиболее устойчивая стратегия достижения поставленной цели имеет вид: х1=3332 ед., х4=667 ед. При полученном плане производства вероятность достижения цели будет равна 47,5%. Рассмотрим первую подзадачу. Если в данном примере считать, что отчетный период длится месяц, т.е. фонд рабочего времени на одного рабочего с учетом простоев составляет 167 часов, то среднесписочная численность работников составляет 6 человек. Ставка (оклад) составляет 1100 руб. в месяц, или 6,6 руб. в час. Если учесть, что каждый неиспользованный человеко-час стоит 6,6 руб., то, решая соответствующую задачу, получаем: оптимальное по устойчивости решение не меняется, т.к. имеющийся фонд рабочего времени и без учета стоимости неиспользованных человеко-часов расходуется полностью. А если считать, что стоимость хранения и поддержания в пригодном для использовании состоянии сырья второго вида стоит 1,5 руб. за единицу, то оптимальный по устойчивости производственный план сильно изменяется: в данном случае выгодно все имеющиеся ресурсы бросить на производство продукции №4 и производить ее в количестве 2000 единиц; при этом устойчивость относительно поставленной цели составляет 39,2%. Полученное в задаче максимизации устойчивости относительно поставленной цели решение, если его подставить в ограничения, показывает, что дефицитными являются следующие ресурсы: сырье первого вида, рабочая сила, рынок сбыта. Предположим, что есть возможность увеличить максимальный объем сбыта до 7000 единиц путем проведения рекламной акции стоимостью в 4500руб. (цены условны) *. Тогда оптимизационная модель имеет вид:
Для простоты вычислений не будем учитывать потери от недоиспользования сырья. Решение имеет вид Чтобы не гадать, как нам подобрать оптимальные количества ресурсов, решим для данного примера соответствующую задачу:
Здесь Заметим также, что поставленная задача актуальна не только для рассматриваемой здесь стохастической целевой функции, но и для ее детерминированного линейного или нелинейного вида, причем ее можно решать как при имеющихся в распоряжении предприятия объемов ресурсов, так и при планировании производства, ориентированного на рынок, когда ограничения по видам ресурсов еще не определены*. Задача выбора оптимальной стратегии возникает и на макроуровне экономической системы. Одним из примеров является конкурсный отбор инвестиционных проектов на размещение кредитных ресурсов регионального бюджета. Постановка задачи такова: пусть определена цель развития региональной экономики как набор желаемых значений определенный параметров состояния экономической системы. На конкурс по размещению кредитных ресурсов регионального бюджет представлен ряд инвестиционных проектов, реализация которых сулит достижение определенных значений параметров цели, но каждый проект обладает определенной устойчивостью, т.е. вероятностью, с которой достигаются объявленные значения параметров цели. Задача состоит в том, чтобы разработать такую стратегию кредитования, при которой поставленная цель достигалась с наибольшей вероятностью. Итак, пусть цель развития региональной экономики на ближайшую перспективу задана следующим образом: уровень безработицы должен быть не выше определенного значения N, средняя заработная плата по региону должна быть не ниже V, сумма налоговых поступлений – не ниже T и так далее. Каждый инвестиционный проект, в случае реализации, предполагает открытие n рабочих мест, поступление в бюджет t ден. ед. налогов и т.д., т.е. существует зависимость значений показателя цели от стратегии кредитования. В данном случае стратегия кредитования представима в виде вектора
где
где pi – показатель устойчивости i-го инвестиционного проекта, n – число кредитуемых проектов в рамках рассматриваемой альтернативы (стратегии). Однако каждый проект имеет определенную стоимость реализации сi, а объем кредитных ресурсов регионального бюджета ограничен суммой М. Поэтому в систему ограничений должно быть включено условие:
Таким образом, имеем задачу линейного программирования, решение которой даст оптимальную стратегию. Пример: На конкурс по размещению кредитных средств регионального бюджета предлагаются пять проектов, обладающих характеристиками, приведенными в Т а б л и ц е 6.6: Цель развития региона, которую планируется достичь путем кредитования инвестиционных проектов, характеризуется следующими параметрами: открыть не менее 200 новых рабочих мест, обеспечить поступление в бюджет региона не менее 65000 руб. Объем кредитных ресурсов области не превышает 70000 руб. Требуется указать стратегию, наиболее вероятно приводящую к достижению поставленной цели. С точки зрения устойчивости относительно поставленной цели, критерием выбора наилучшего решения в данной ситуации будет произведение показателей устойчивости тех проектов, которые в итоге будут профинансированы. Т а б л и ц а 6.6 Индивидуальные характеристики проектов
Математическая модель задачи имеет вид:
Путем перебора возможных сочетаний проектов, находим сочетание, максимизирующее целевую функцию и удовлетворяющее всем условиям. Решение задачи состоит в том, что наиболее целесообразно кредитовать проекты №№ 1,3 и не кредитовать проекты №№ 2,4,5. Это "стоит" 45900 руб., позволяет открыть 219 новых рабочих мест и получить 68370 руб. в виде налогов. Неизрасходованные средства можно оптимально разместить, пользуясь предложенным методом. Для этого нужно либо сформулировать новую задачу, либо ужесточить ограничения. Таким образом, при оптимальном управлении размещением кредитных ресурсов регионального бюджета можно выстраивать последовательность целей оптимальным образом, т.е. так, чтобы поставленные цели достигались с наибольшей вероятностью.
* Отметим, что данная проблема неактуальна, когда инвестиционный проект кредитуется однажды и необходимости ни в рефинансировании, ни во вторичном кредитовании нет. Тогда на покрытие кредита, очевидно, выгоднее всего бросить все свободные денежные средства на первых этапах реализации проекта, так как чем скорее тело кредита и проценты будут выплачены, тем больше будут интегральные показатели его эффективности. * С учетом налогов, которые берутся с валовой выручки; учтено также поступление 250 тыс. руб. кредитных средств ** С учетом отчислений из ФОТ *** С учетом отчислений из ФОТ * Налоги в данном примере не учитываются во избежание излишних технических сложностей, не меняющих сути дела. * Несмотря на то что выплата дивидендов происходит по фактическим результатам функционирования проекта, для принятия решения о его начале необходим предварительный просчет выгод от его реализации. * В противном случае один критерий будет необоснованно преобладать над другим. * Например, если «придумать» целевую функцию вида R+A, то прямой резон обнулить R и получить при этом неограниченные приращения А. Аналогичная ситуация наблюдается, когда целевая функция имеет вид, например, . Такие виды целевых функций заведомо негодны. * Покрытие расходов, которые несут акционеры в связи с функционированием проекта, учитывается в общих издержках. На графике показаны чистые дивиденды. * Разумеется, при расчете платы за дополнительные единицы ресурсов следует учитывать ту ее часть, которая уже заложена в себестоимость, и с учетом которой рассчитываются параметры удельной прибыльности. Дополнительные издержки, не пропорциональные объему поставляемого ресурса, возникают вследствие необходимости дополнительной подготовки производства, связанной с приемкой, хранением и обработкой дополнительной партии ресурса, а также как результат действия механизмов спроса-предложения на сырьевом рынке. В этой связи можно поставить задачу оптимального по устойчивости управления тарифами , которое в ряде ситуаций можно осуществлять, внедряя определенные технологические решения, которая решается в соответствии с методологией, изложенной в данном исследовании. * Для простоты мы не стали разделять рабочую силу по разрядам и специальностям, хотя на практике такое разделение следует отражать в модели. * Или, например, сбыт продукции увеличивается за счет посредников, которые берут свои комиссионные. * Естественно, в данном случае удельные затраты ресурсов на производство единицы продукции не учитываются, и параметры целевой функции представляют собой фактически цены реализации производимых товаров, а не их удельные прибыльности. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
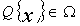(6.1)
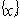– множество управляемых параметров организации всех уровней управления, а 
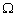– изображающая область цели. Устойчивость относительно поставленной цели, очевидно, есть функция как от 
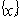, так и от 
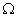, поэтому управлять устойчивостью можно, управляя данными компонентами целеуказания. Формально 
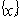-управление не отличается от 
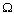-управления, однако эти виды управления имеют различный экономический смысл. Если 
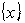-управление имеет место при заданной цели и обеспечивает максимальную вероятность ее достижения, то при 
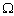-управлении процессы целеуказания (и возможно целеполагания) и исполнения поставленной цели совмещаются во времени, поэтому в ходе 
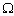-управления корректируются первоначальные установки цели исходя из возможностей управляемой организации по ее достижению. А если меняются установки цели, то сразу же возникает вопрос о целесообразности действий по достижению измененной цели: может быть, измененная цель достигается с наибольшей вероятностью, но ее достижение не принесет желаемого результата. Поэтому целевой функцией 
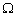-управления является некое сочетание 
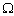и устойчивости относительно данной 
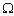, например математическое ожидание границ изображающей области цели. Однако 
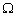-управление представляет значительно меньший практический интерес, чем
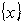-управление; кроме того, при управлении устойчивостью относительно поставленной цели предполагается, что целеуказание уже осуществлено, что сужает круг применения 
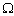-управления до немногих малоинтересных задач. Поэтому в дальнейшем изложении будут рассматриваться только задачи 
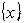-управления.
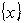- управления зависит от параметров целеуказания, в том смысле что управляемыми переменными являются только управляемые параметры целеуказания. Как правило, целеуказание содержит явным образом лишь некоторые параметры организации, причем управляемыми из них являются не все, тем самым возможности 
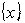- управления сокращаются. Однако процесс 
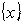- управления легко формализуется, и построенная модель позволяет получить точные результаты.
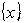-управления такова:
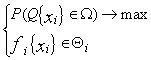(6.2)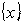
-управления в случае функционирования организации по неизменной программе необходимо вначале определить параметры, которыми можно управлять и составить целеуказание как функцию от управляемых параметров. Несмотря на кажущуюся тривиальность этого положения, определение управляемых параметров и задание ограничений – довольно сложная процедура. В каждой конкретной задаче отыскивается свой набор параметров управления, однако увеличение общности в постановке задачи неминуемо накладывает жесткие ограничения на выбор этих параметров. В самом деле, если рассматривать экономические системы, выбор достаточно узок. Управлять ценой довольно проблематично, учитывая возможную неблагоприятную реакцию рынка. Управлять объемами сбыта продукции можно, но как бы такое управление не оказалось беспочвенным прожектерством, так как еще не факт, что реальные объемы сбыта будут близки к выбранным. То же самое относится и к прямым издержкам. Можно эффективно управлять условно постоянными затратами, определив их минимально возможный уровень, однако конкретные ситуации накладывают довольно жесткие ограничения на выбираемые значения данного параметра. Кроме того, при управлении перечисленными параметрами приходится вводить в модель дополнительные ограничения и условия, которые отражают изменение состояния управляемой организации при выбранных значениях параметров. Например, варьировать цену без значимых изменений объема сбыта можно лишь в определенном интервале, вне этого интервала работают рыночные механизмы – при повышении цены объем сбыта снижается, т.е. необходимо промоделировать зависимость объема сбыта от цены.
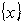-управления устойчивостью, могут быть проанализированы несколько задач, относящихся к данному классу, затрагивающих различные аспекты функционирования организаций по достижению поставленных целей. В этой части исследования будут рассматриваться следующие задачи:
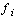ден. ед. свободных средств, покрыв все расходы, связанные с деятельностью, и погасив все текущие финансовые обязательства*. Если рассматривать данную проблему с позиций устойчивости относительно поставленной цели, то при заданном целеуказании необходимо максимизировать вероятность достижения поставленной цели, управляя какими-либо параметрами функционирования, в данном случае – графиком выплат задолженности по полученным кредитам. Оптимизационные задачи, поставленные для других параметров управления, решаются аналогично.
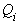и издержки, не связанные с обслуживанием задолженности по кредиту: 
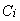– постоянные и 
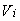– переменные (детализация данных величин, учет налогов, амортизации и т.п. для поставленной задачи несущественна), которые варьируют в установленных пределах, и выплачивает проценты по кредиту в размере 
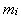ден. ед.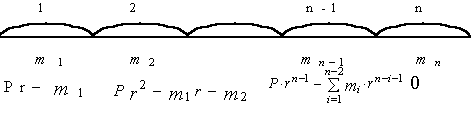
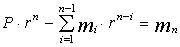(6.3)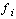
ден. ед. свободных средств, целеуказание будет иметь вид:
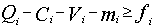(6.4)
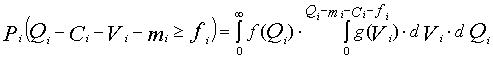(6.5)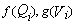
– функции плотности распределения случайных величин дохода и переменных затрат, не связанных с обслуживанием кредита.
, где n – число отчетных периодов, лежащих в интервале планирования. Таким образом, наша задача в формальной постановке имеет вид: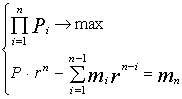
(6.6)
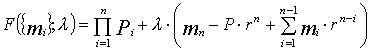(6.7)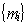
, получаем, что суммы выплат по периодам, 
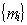, должны удовлетворять системе уравнений:
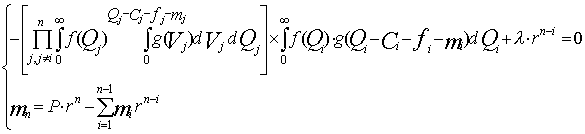(6.8)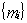
говорит о том, что сумм выплат могут быть не только положительными, но и отрицательными (дополнительные заимствования или, в зависимости от периода, отвлечение реинвестированных свободных средств). Если дополнительное финансирование исключено, необходимо учесть данное обстоятельство непосредственно в ограничениях или пересмотреть план рефинансирования отдельных этапов проекта, так как в данном случае недопустимый по этим соображениям график выплат – есть следствие не ошибочного метода решения, а противоречивости исходных данных. Как правило эта трудность устраняется путем «разбрасывания» различных этапов реализации проекта по всему горизонту планирования, что, естественно, снижает интегральные показатели эффективности проекта, однако делает план более реальным.
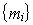находится, в соответствии с предложенным методом, из системы уравнений:
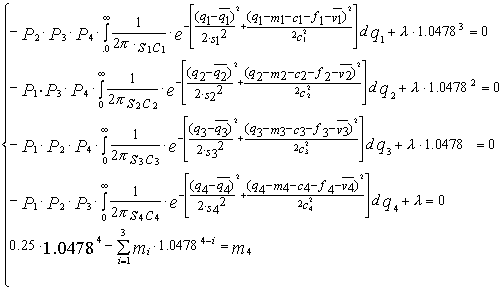(6.9)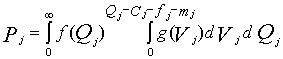
, 
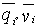– ожидаемые (расчетные) значения доходов и переменных издержек в i-м периоде, 
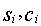– их среднеквадратические отклонения в i-м периоде. Решение данной задачи дает
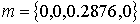млн. руб. Таким образом, оптимальный по устойчивости график погашения кредита состоит в том, что кредит следует погасить единовременно, заплатив 287,6 тыс. руб. в течение период 5-8.2002 г., при этом устойчивость относительно поставленной цели составляет 75,5% в период 9-12.2001 г., в следующие периоды, соответственно, 83,9%, 77,8% и 70,8%, итого 34,9%. Заметим, что если распределить суммы выплат каким-либо другим рациональным способом, то устойчивость падает. Например, если распределить выплаты пропорционально величине получаемого дохода за вычетом всех издержек, не связанных с выплатой кредита, т.е. платить по графику
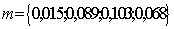, то устойчивость относительно поставленной цели составит 33,5%.
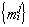– выплаты по j-й кредитной линии в i-м периоде, 
, 
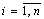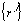– коэффициенты удорожания кредитов, полученных по j-й кредитной линии за расчетный период (месяц, квартал, год), 
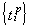– суммы операций по инвестированию и депонированию свободных денежных средств по р-му объекту инвестирования, 
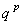– коэффициент возрастания вложенных в р-й объект средств за расчетный период. Тогда целеуказание имеет вид:
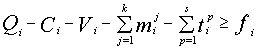(6.10)
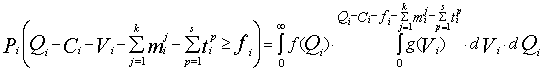(6.11)
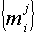и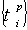 
, и ограничений, описывающих экономический смысл вводимых переменных:
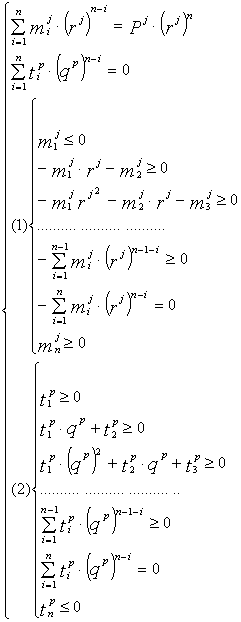(6.12)
. Следующие ограничения группы (1) вытекают из того, что за кредиты, полученные в предыдущих периодах, нельзя переплачивать; иначе получится, что это никакой не кредит, а депонент: предприятие сначала «переплачивает» за полученный ранее кредит, а та разница, которая переплачена за ранее полученный кредит, возрастает в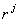 
раз за каждый период и, естественно, возвращается предприятию в конце периода планирования. Этого не допускает ни один банк, так как ставка процента по кредиту значительно выше, чем ставка процента по депоненту. Группа ограничений (2) описывает движение депонированных средств. А на депонент, в отличие от кредита, сначала кладут, а потом берут, о чем говорит ограничение 
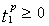. Следующие ограничения группы (2) говорят о том, что вы никогда не получите больше, чем вложили в предыдущие периоды, иначе слишком дешевое выходит кредитование, если вначале взять большую сумму, а затем возвращать ее под процент, установленный на депоненте; этого тоже нигде не бывает.
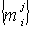, если соответствующие кредитные линии не допускают повторного кредитования, и ограничениями на объемы финансовых операций в течение периода, т.к. на их осуществление может не хватить ресурсов. Особенно это актуально для кредитов, т.к. в любом случае их можно получить только при наличии залога, в несколько раз превосходящего по величине необходимую сумму. Это также актуально и для осуществления финансовых вложений – сначала нужно расплатиться со всеми текущими обязательствами, а потом вкладывать.
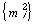, ставка процента по которой составляет 65% годовых, т.е. 18,2% в отчетный период, с нулевой начальной суммой. Предположим, что у предприятия есть возможность депонировать свободные денежные средства в коммерческом банке под 20% годовых, или 6,3% в отчетный период и получать доход по графику 
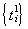. Причем величина взятого кредита не может превосходить по величине 400 тыс. руб., а на депонент можно класть суммы, составляющие не более 50% от величины чистой прибыли без учета налогов*. Тогда, решив задачу с новыми входными данными, находим оптимальные графики обслуживания кредита и депонирования свободных денежных средств: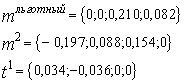
,
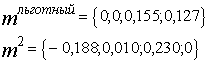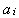денежных единиц. Сохраняя ранее использовавшиеся обозначения, запишем целеуказание:
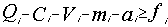(6.13)
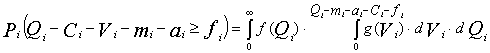(6.14)
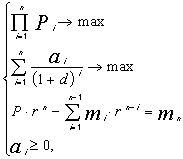(6.15)
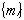, если можно пользоваться только одной кредитной линией. Метод решения задачи зависит от выбранного варианта конструирования синтетической целевой функции.
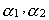, не обязательно составляющие в сумме единицу, но выбираемые с таким расчетом, чтобы критерии устойчивости и доходности по акциям были однопорядковыми величинами*. Тогда оптимизационная модель имеет вид:
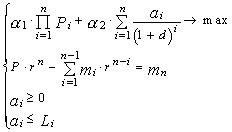(6.16)
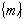и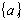 
, записанного в виде соотношений между параметрами задачи, не приводится. Заметим, что если веса критериев не принадлежат области согласования интересов менеджеров и акционеров, оптимальное решение будет получено с учетом интересов лишь одной стороны – менеджеров или акционеров, а значит оно заведомо неоптимально.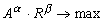
,
.
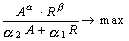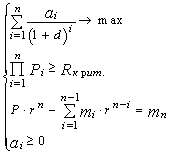(6.17)
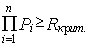эквивалентно ограничению 
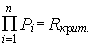, так как при возрастании устойчивости убывает доходность, и наоборот, и функции устойчивости и доходности непрерывны, поэтому при максимизации функции доходности при ограничении на устойчивость значение последней «упрется» в критическое. Если это так, то решение задачи находится из уравнений:
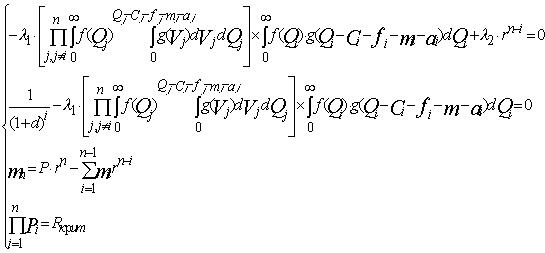(6.18)
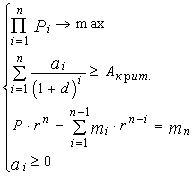(6.19)
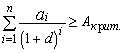эквивалентно ограничению 
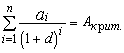, а система ограничений также может быть дополнена дополнительными ограничениями на суммы выплат процентов и дивидендов в некоторых периодах. В данном случае решение задачи находится из уравнений:
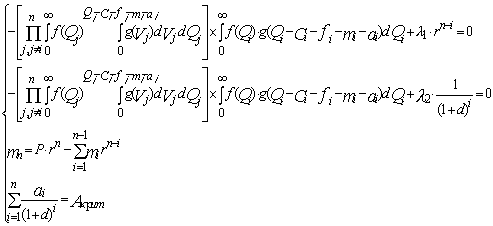(6.20)
(обозначения сохранены), или среднее геометрическое показателей устойчивости в отчетных периодах на протяжении всего горизонта планирования,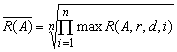 
График данной функции имеет вид, изображенный на рисунке 6.2: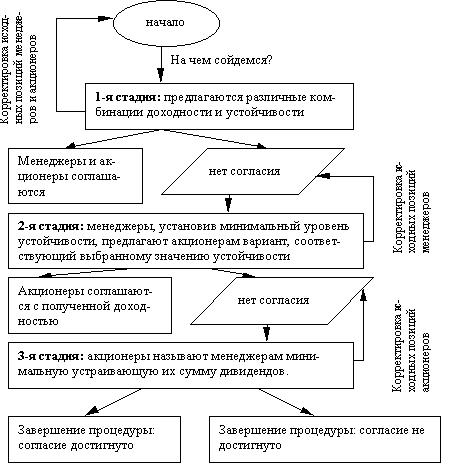
может меняться в каждом отчетном периоде на протяжении всего периода целеуказания. Поэтому при решении задачи 
-управления в данном случае оптимальное по устойчивости целеуказание задается с учетом возможности изменения структуры 
. Задачу 
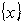-управления при «включенном» текущем управлении можно ставить практически для любой модели управления, которая допускает математически формализуемую связь параметров целеуказания и устойчивости относительно поставленной цели. Суть ее в том, что даже при «включенном» текущем управлении приходится из множества допустимых стратегий на будущий отчетный период приходится выбирать одну, так как даже самая гибкая производственная система при функционировании не сразу может быть настроена на изменившееся управляющее воздействие. Приведем примеры.
-управления позволяет выбрать оптимальный с точки зрения устойчивости вариант стратегии функционирования управляемой системы из множества вариантов, приводящих к поставленной цели, то есть такую стратегию, реализация которой с наибольшей вероятностью приведет к поставленной цели. Задача выбора оптимальной по устойчивости стратегии заключается в выборе стратегии, при которой фазовая траектория системы с наибольшей вероятностью проходит через изображающую область цели, причем стратегия может не входить в счетное множество возможных оптимальных при определенных параметрах целевой функции стратегий, а быть, например, линейной комбинацией нескольких стратегий. Требование максимизации устойчивости стратегии принципиально отличается от требования максимизации количественного ее результата, так как в данном случае учитывается неполная определенность влияющих параметров внешней среды, что полностью игнорируется в задачах максимизации результата. И хотя в качестве цели можно задать максимизацию результата, стратегия решения данной проблемы может быть настолько неустойчивой, что возмущающие воздействия внешней среды сведут обещанный максимальный результат на нет. В этом случае гораздо естественнее с самого начала задать цель и разработать наиболее устойчивую стратегию ее достижения. Впрочем, с помощью анализа устойчивости можно находить стратегии, максимизирующие ожидаемый с учетом возмущающих воздействий внешней среды результат, т.е. решать задачу оптимального целеуказания, или задачу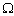 
-управления.
руб. Оптимальной стратегией функционирования предприятия при точно определенных параметрах удельной прибыльности является стратегия, доставляющая максимум целевой функции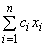 
, где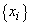 
– объемы выпуска продукции при ограничениях на используемые ресурсы, производственные мощности, рынок сбыта и т.п., заданных линейной моделью вида 
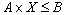. Однако при неопределенных параметрах удельной прибыльности целевой функцией разумно считать не максимум прибыли, а максимум устойчивости относительно поставленной цели, выбирая стратегию, максимизирующую устойчивость. Рассмотрим простейший случай, когда целеуказание происходит относительно прибыли, т.е. целью функционирования в некотором периоде является получение прибыли не менее Zруб.; для случаев задания цели по другому критерию предлагаемый алгоритм также справедлив. В этом случае оптимизационная модель имеет вид:
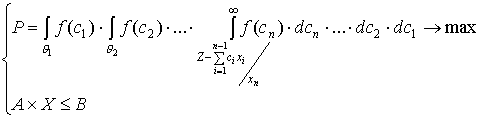(6.21)
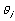– область допустимых значений удельной прибыльности i-того товара, 
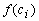– плотность распределения ее значений. В результате решения задачи находится оптимальный по устойчивости производственный план.
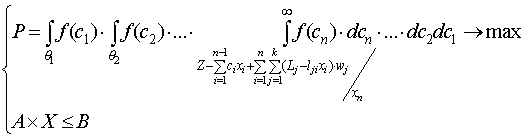(6.22)
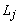– запас сырья j-го вида, 
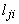– норма расхода сырья j-го вида на производство продукции i-го вида, 
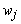– потери от недоиспользования единицы сырья j-го вида. Это актуально для таких видов ресурсов, как рабочая сила, т.к. недоиспользованным рабочим приходится платить или их ставку, или пособие, оборудование, т.к. амортизация начисляется вне зависимости от степени использования оборудования в отчетном периоде, и некоторых других видов ресурсов.
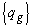единиц, где g – количество используемых ресурсов, заплатив за каждую дополнительную единицу определенный тариф 
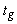, и проследить, как в этом случае изменится устойчивость относительно поставленной цели*. Суть второй подзадачи заключается в рассмотрении и оценке эффективности увеличения запасов дефицитных видов сырья по критерию устойчивости относительно поставленной цели. В этом случае оптимизационная модель имеет вид:
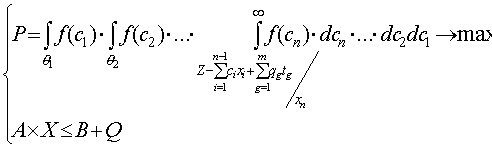(6.23)
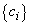извлекается эта доля, а ограничение на соответствующий ресурс можно убрать. Заметим, что возможно поставить и решить комбинированную из этих подзадач задачу, целевая функция которой будет содержать элементы целевых функций этих подзадач:
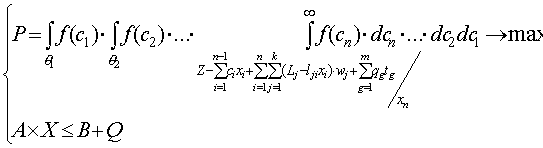(6.24)
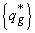, при которых устойчивость относительно поставленной цели будет максимальной. В этом случае оптимизационная модель имеет вид:
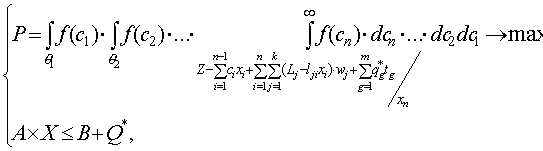(6.25)
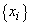добавляются параметры 
.
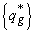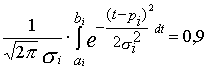(6.26)
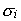– среднеквадратичное отклонение удельной прибыльности i-го товара, ai, bi – соответственно, нижняя и верхняя границы доверительного интервала. Имеем: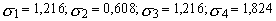 
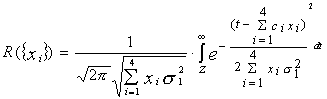. (6.27)
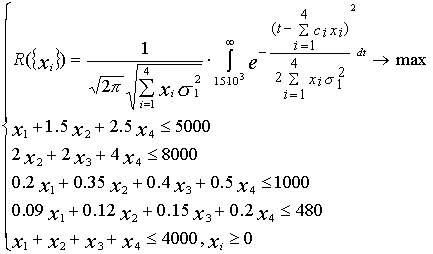(6.28)
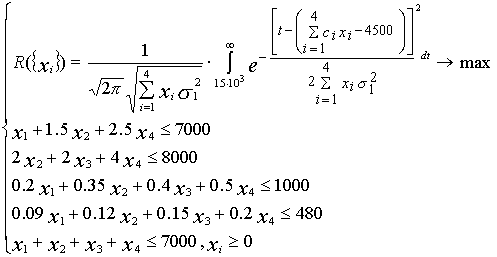(6.29)
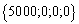, которое доставляет устойчивость 23%. Из этого следует, что такая рекламная акция неэффективна, так как в этом случае устойчивость значительно ниже. Улучшить ситуацию может появление посредника, которому отдадим, скажем, 15% от выручки, однако и в этом случае устойчивость, повышаясь до 35,6% , все равно меньше устойчивости базовой стратегии. Это происходит из-за того, что при увеличении объема рынка сбыта до 7000 единиц дефицитным стало сырье 1-го вида.
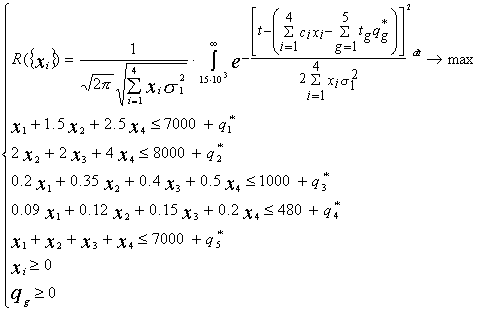(6.30)
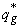– привлекаемые дополнительно количества ресурса g-го вида, 
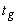– цена единицы привлекаемого ресурса. Заметим, что в данном случае можно не учитывать потери от недоиспользования ресурсов, т.к. 
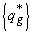при оптимальном решении будут такими, чтобы ресурсы использовались полностью – иначе зачем платить за ресурс, который окажется лишним. Модель ограничений может быть дополнена ограничениями на привлекаемые дополнительно виды сырья, если нужно. Если считать, что за привлечение дополнительной единицы ресурсов 1 и 2 приходится платить, соответственно 1,5 и 1 руб., за каждый дополнительный человеко-час рабочего времени платить по 7 руб., а за каждый машино-час – 6,4 руб. (это может быть арендная плата за дополнительное оборудование и производственные площади), а посреднику отдавать 15% от выручки, то решение имеет вид 
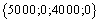, а устойчивость относительно поставленной цели составляет 49,5%, что показывает достаточно высокую эффективность оптимизации, учитывая большие в сравнении с удельными прибыльностями товаров затраты на привлечение дополнительных ресурсов.
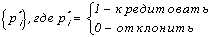. Таким образом, цель развития представима в виде системы ограничений:
(6.31)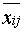
– вектор, компонентами которого являются количественные результаты от функционирования i-го проекта по j-му параметру цели (например, сколько рабочих мест открывается в рамках определенного проекта и т.д.), Z1, Z2, ... – параметры цели. Заметим, что в данном случае цель задается не столько в форме структурной компоненты целевой функции (как это происходит в приведенных выше задачах 
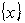-управления), сколько в виде ограничений. Условие оптимальности стратегии полностью продиктовано требованием максимальной устойчивости ее относительно поставленной цели и имеет вид:
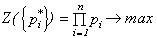(6.32)
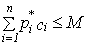(6.33)
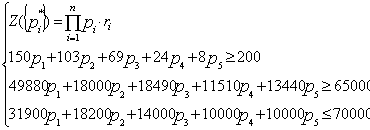(6.34)