«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Рынок ценных бумаг Конспект лекций. Таганрог: Изд-во ТРТУ, 1998. 135с. Тема 2. Акции 2.5. Модели оценки акцийВопрос оценки акций тесно связан с ее жизненным циклом, который охватывает выпуск, первичное размещение и обращение акций. В период выпуска акция характеризуется номинальной стоимостью. Номинальная стоимость акции - это стоимость акции, указанная в уставе акционерного общества, равная стоимости доли уставного капитала общества, оплата которой удостоверяется данной акцией. Номинал всех акций должен быть одинаковым и обеспечивать всем держателям равный объем прав. В период первичного размещения акция характеризуется эмиссионной ценой - это цена акции, по которой ее приобретает первый держатель. По существующему законодательству эмиссионная цена акций едина для всех первых покупателей, может превышать номинальную стоимость или быть равной ей. При учреждении акционерного общества оплата акций его учредителями производится по номинальной стоимости. При всех последующих выпусках оплата акций производится по рыночной цене. Превышение эмиссионной стоимости акций над их номинальной стоимостью является эмиссионным доходом (эмиссионной выручкой). По законодательству он присоединяется к собственному капиталу акционерного общества. Рыночная (курсовая) цена - это цена, по которой акция продается и покупается на вторичном рынке. Она может устанавливаться на биржевом или внебиржевом рыке. Рыночная цена, установленная на бирже, отражает действительную цену акции при условии большого объема сделок. Котировка предполагает наличие двух цен: - цену приобретения или цену спроса (bid price) - цена бид; - цену предложения (offer price) - офферта. Разница между ценой предложения и ценой спроса называется спрэдом. Сделки купли-продажи заключаются по фактическим (курсовым) ценам при совпадении интересов покупателя и продавца на определенный момент биржевых торгов. Цена, по которой совершается первая сделка, называется ценой открытия, последняя - цена закрытия. В течение дня формируются минимальная и максимальная цены. Показатель, отражающий среднюю цену акции по определенной совокупности компаний, называется биржевым (торговым) индексом. Индекс позволяет инвесторам оценивать как состояние фондового рынка в целом, так и надежность собственных активов. В зарубежной практике распространен следующий способ расчета рыночной (курсовой) стоимости обыкновенных акций (2.3):
где Pp - рыночная цена акции; Kp - курс акции; Н - номинал акции. Курс акции может быть определен в результате сопоставления дивиденда, выраженного в процентах от номинальной стоимости, и ставки ссудного процента (2.4):
Если дивиденд выше ставки ссудного процента, то курс больше единицы, и акции продаются по цене выше номинальной и наоборот. Однако в отечественной практике данный метод не применим, поскольку ставки ссудного процента не сопоставимы с уровнем рентабельности большинства акционерных обществ и, как следствие, со ставками дивидендов. При стоимостной оценке акций важную роль играет их книжная или балансовая стоимость. Она определяется экспертами на основе оценки собственных (чистых) активов акционерного общества следующим образом (2.5):
Порядок определения стоимости чистых активов. Собственные (чистые) активы - это величина, определяемая путем вычитания из суммы активов организации, принимаемых к расчету, суммы ее обязательств, принимаемых к расчету. В соответствии с федеральным законом "Об акционерных обществах" стоимость чистых активов общества оценивается по данным бухгалтерского учета. Если по окончании финансового года в соответствии с годовым бухгалтерским балансом, предложенным для утверждения акционерам общества, или по результатам аудиторной проверки стоимость чистых активов оказывается меньше величины уставного капитала, то общество обязано объявить об уменьшении стоимости уставного капитала до величины чистых активов. Если стоимость чистых активов оказывается меньше величины минимального уставного капитала, то общество обязано объявить о своей ликвидации. Активы, участвующие в расчете, - это денежное и неденежное имущество акционерного общества, в состав которого включаются по балансовой стоимости следующие статьи: - внеоборотные активы (за исключением балансовой стоимости собственных акций общества, выкупленных у акционеров); - запасы и затраты, денежные средства, расчеты и прочие активы, показываемые во втором разделе бухгалтерского баланса, за исключением задолженности участников (учредителей) по их вкладам в уставный капитал и балансовой стоимости собственных акций, выкупленных у акционеров. Пассивы, участвующие в расчете, - это обязательства акционерного общества, в состав которых включаются следующие статьи: - целевые финансирование и поступления; - долгосрочные обязательства банкам и иным юридическим и физическим лицам; - краткосрочные обязательства банкам и иным юридическим и физическим лицам; - расчеты и прочие пассивы (кроме сумм, отраженных по статьям "Доходы будущих периодов" и "Фонды потребления"). Таким образом, обращение акций предполагает существование следующих их стоимостных характеристик: - номинальная стоимость; - эмиссионная цена; - рыночная (курсовая цена); - балансовая стоимость. Оценка инвестиционной привлекательности обыкновенных акций может быть проведена с использованием ряда показателей и моделей. Доходность акции оценивается с учетом всех поступлений, которые может получить инвестор в период инвестирования денежных средств в акцию. Общий доход по акции складывается из следующих элементов: - периодически выплачиваемых дивидендов; - изменений стоимости акции за соответствующий период (курсовая разница). Текущая доходность акции без учета ее реализации рассчитывается как отношение суммы полученного дивиденда к цене приобретения акции (2.6).
где Т - период инвестирования в календарных днях. Кроме того, можно рассчитывать рыночную текущую доходность, которая будет зависеть от уровня цены, существующей на рынке в каждый данный момент времени (2.7). Рыночная текущая доходность= Если период инвестирования заканчивается реализацией акции, то доходность рассчитывается с учетом совокупных дивидендов и изменения курсовой стоимости (2.8).
Доходность инвестора является конечной, поскольку он реализовал свою ценную бумагу, и период инвестирования закончен. Если инвестиционный период не включает выплаты дивидендов, то доход (убыток) образуется как разница между ценой покупки и продажи. Модели определения истинной стоимости акций строятся на определении их текущей стоимости (метод капитализации дохода - capitalization of income method of valuation). Этот метод предполагает, что истинная или внутренне присущая стоимость любого капитала основана на финансовом потоке, который инвестор ожидает получить в будущем в результате обладания этим капиталом. В основе определения текущей стоимости лежит формула дисконтирования, чтобы учесть не только изменение стоимости денег со временем, но также и фактор риска. Алгебраически истинная стоимость капитала равна сумме приведенных стоимостей ожидаемых поступлений и выплат:
где Po - текущая стоимость акции в некоторый момент времени (t=0); Dt - периодические дивидендные выплаты по акции; i - процентная ставка дисконтирования. Если затраты на приобретение финансового актива в момент времени t=0 составляют Pp, то его чистая приведенная стоимость (net present value, NPV) равна разности между его истинной стоимостью и затратами на приобретение:
Приобретение акции рассматривается как приемлемое в случае, если В отдельных источниках модель, представленная формулой (2.9), называется моделью дисконтированных дивидендов (dividend discount model, DDM). В этом равенстве ставка дисконтирования предполагается постоянной в течение всего времени. При использовании данного равенства для определения истинной цены обыкновенной акции могут возникнуть определенные трудности, так как инвестор должен предсказать все последующие дивиденды (иными словами, необходимо прогнозировать бесконечный поток платежей). Хотя это может показаться неразрешимой задачей, при некоторых предположениях с ней можно справиться. Данные предположения в основном связаны с темпом роста дивидендов. В этом случае дивиденд на одну акцию в момент времени t равен величине дивиденда в момент t-1, умноженной на темп роста дивидендов
что эквивалентно следующей записи
Применяемые модели дисконтирования дивидендов различаются в зависимости от предположений о темпе роста дивидендов. Простейший случай - модель нулевого роста (zero-growth model). В данной модели дивиденд предполагается неизменным (фиксированное число) и формула (2.9) принимает следующий вид:
Далее, пользуясь свойством бесконечных рядов из курса математического анализа, получим, что при Di >0
С учетом последнего из равенства (2.13) получим следующую формулу для модели нулевого роста:
Формула расчета NPV принимает следующий вид:
Модель постоянного роста (constant growth model) - это модель, в которой предполагается, что дивиденды будут расти от периода к периоду в одинаковой пропорции, т.е. с одинаковым темпом роста g:
В этом случае формула расчета текущей стоимости принимает следующий вид:
С учетом того, что
Данная формула применима при g < i. Модель переменного роста (multiple-growth model). Главная особенность данной модели - это период времени в будущем, обозначаемый через Приведенная стоимость дивидендов, выплачиваемых до периода
Приведенная стоимость прогнозируемых дивидендов после момента времени
Общий расчет приведенной стоимости акции
Если инвестор предполагает в будущем продать акцию, то используется оценка акции с учетом конечного срока владения
где Ppn - цена продажи акций в году n. Инвесторы также применяют две модели дисконтирования дивиденда, получившие название двухэтапной и трехэтапной моделей. Двухэтапная модель предполагает, что до некоторого момента времени |
||
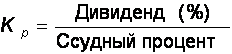 . (2.4)
. (2.4) (2.5)
(2.5)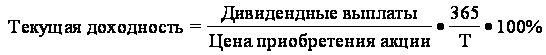 , (2.6)
, (2.6)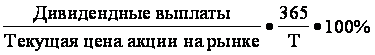 . (2.7)
. (2.7)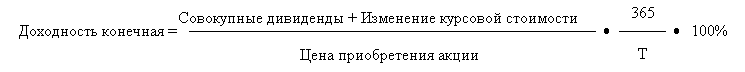 (2.8)
(2.8)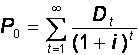 , (2.9)
, (2.9)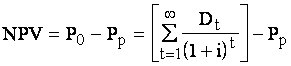 . (2.10)
. (2.10)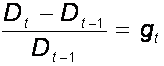 . (2.12)
. (2.12)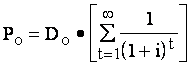 . (2.13)
. (2.13) . (2.14)
. (2.14)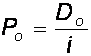 . (2.15)
. (2.15)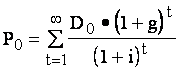 , (2.18)
, (2.18) . (2.19)
. (2.19)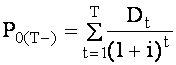 . (2.20)
. (2.20)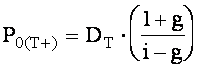 . (2.21)
. (2.21)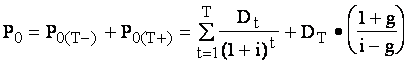 . (2.22)
. (2.22)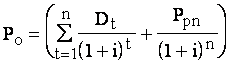 , (2.23)
, (2.23)