«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Финансовые и коммерческие расчеты на ЭВМ Конспект лекций.Таганрог: Изд-во ТРТУ, 2005 1.ТЕОРИЯ ПРОЦЕНТОВ 1.3. Дисконтирование по сложной ставке процентов
Дисконтирование по сложной ставке процентов — процесс, обратный во времени процессу наращения (компаундинга) по сложной ставке процентов. Если при наращении изменение первоначальной суммы Р происходит дискретно, скачками, в конце очередного периода начисления процентов, то процесс дисконтирования будущей суммы S также происходит скачкообразно, в обратном направлении, со скачком в конце очередного периода дисконтирования. В конце первого периода дисконтирования величина текущей стоимости суммы S равна S/(1+ iT), в конце второго периода - s/(1+iT )2 и т. д. После п циклов дисконтирования текущая стоимость суммы S равна (ср. с (1.2.1)): где v При начислении процентов т раз в году дисконтный множитель за период равен: v Дисконтирование при непрерывном начислении процентов также описывается формулой (1.2.13), где время изменяется непрерывно, в отличие от дискретного начисления процентов т раз в год, когда время изменяется дискретно, с шагом1/т. Очевидно, непрерывная кривая (1.2.13) является огибающей для закона дискретного дисконтирования суммы Sпри любом числе периодов дисконтирования в году исходя из одинаковой эффективной годовой процентной ставки.
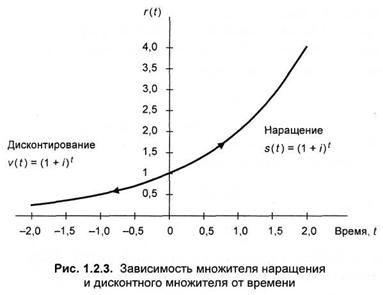
Чтобы единым образом описать приведение суммы к определенному моменту времени, введем, как и в разделе 1.1, множитель приведения, который равен множителю наращения при приведении к будущему моменту времени и дисконтному множителю при приведении к предшествующему (настоящему) моменту времени. Удобно совместить начало шкалы времени с моментом времени, когда задана сумма. Тогда наращению соответствует положительная часть оси времени, а дисконтированию — отрицательная. Множитель приведения для непрерывной процентной ставки можно записать с учетом (1.2.13) в виде где s(t) — множитель наращения; v(|t|) — дисконтный множитель.
Зависимость этого множителя от времени, определяемая формулой (1.2.13,а), приведена на рис. 1.2.3 для годовой нормы доходности 30%. |
||
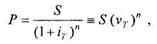 (1.2.12)
(1.2.12)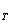 = 1/(1 + iT) — дисконтный множитель за период Т.
= 1/(1 + iT) — дисконтный множитель за период Т.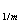 = l/(l + i{m)/m). По аналогии с процессом наращения вводится годовой дисконтный множитель v, что, позволяет записать выражение для текущей стоимости в следующем виде (ср. с (1.2.2), (1.2.3), (1.2.7)):
= l/(l + i{m)/m). По аналогии с процессом наращения вводится годовой дисконтный множитель v, что, позволяет записать выражение для текущей стоимости в следующем виде (ср. с (1.2.2), (1.2.3), (1.2.7)):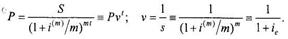 (1.2.13)
(1.2.13)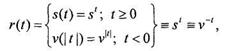 (1.2.13,а)
(1.2.13,а)