«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Финансовые и коммерческие расчеты на ЭВМ Конспект лекций.Таганрог: Изд-во ТРТУ, 2005 1.ТЕОРИЯ ПРОЦЕНТОВ 1.4. Учетная процентная ставка Учетная ставка
В банковской практике при учете (т. е. досрочной покупке) векселей и других денежных обязательств в расчетах исторически используется не ставка ссудных процентов, а так называемая учетная ставка. Учетная ставка связана с антисипативным способом начисления процентов, где плата за кредит, т.е. процентный доход, начисляется авансом при выдаче кредита. В этом случае должнику выдается сумма, уменьшенная на величину процентного дохода, а возврату в конце срока подлежит полная сумма долга. Величина дисконта, скидки с суммы долга, D определяется как разница между суммой, подлежащей возврату – S, и первоначальной суммой ссуды – Р. Отношение этих величин dT называется учетной ставкой за период Т:
Обычно банки указывают годовую (номинальную) учетную ставку d, а учетная ставка за период времени Т до погашения долга определяется по формуле
Тогда
где множитель vT =1-dT =1-dT называется дисконтным множителем за период Т по учетной ставке d.
Расчет стоимости ценных бумаг в электронных таблицах Excel Для расчета стоимости векселя в Excel используется финансовая функция ЦЕНА-СКИДКА. Обращение к функции: ЦЕНА-СКИДКА (дата_соглашения, дата_вступления_в_силу, скидка, погашение, базис). Дата_соглашения – дата соглашения для ценных бумаг, пораженная как дата в числовом формате (дата покупки, учета). Дата_вступления_в_силу – дата вступления в силу ценных бумаг, выраженная как дата в числовом формате (дата погашения). Скидка – норма скидки для ценных бумаг (годовая номинальная учетная ставка). Погашение – цена при погашении (за 100 руб. нарицательной стоимости ценных бумаг). Базис – тип используемого способа вычисления дня (если 0 или отсутствует, то длительность года принимается равной 360 дням). Расчет производится по формуле (1.3.3), где время (в долях года) равно количеству дней от даты продажи до даты погашения, деленному на количество дней в году. Даты продажи и погашения выражаются в числовом формате как номер дня в соответствующей системе (в Excel – с 1 января 1900 г.) с помощью функции ДАТА из блока функций "ДАТА И ВРЕМЯ". Для примера 1.3.2 определим дату учета векселя как 1 января 1998 г., дату погашения – 1 марта 1998 г. В числовом формате эти даты равны соответственно: ДАТА(1998; 1; 1)=35431; ДАТА(1998;3;1)=35490. Тогда учетная стоимость векселя равна: ЦЕНА-СКИДКА (35431; 35490;0,2;10)=9,6667 (тыс. руб.). Наращение по учетной ставке
При антисипативном методе начисления процентов дисконтирование – прямая операция, а наращение по простой учетной ставке – обратная. В последней возникает необходимость при определении суммы, которую следует проставить в векселе, если известна текущая сумма долга. Как следует из формулы (1.3.3), наращение по простой учетной ставке описывается следующей формулой:
Чтобы единым образом описать приведение суммы к определенному моменту времени с помощью учетной ставки, введем, как и в разделе 1.1, множитель приведения, который равен множителю наращения при приведении к будущему моменту времени и дисконтному множителю при приведении к предшествующему (настоящему) моменту времени. Удобно совместить начало шкалы времени с моментом времени, когда задана сумма. Тогда наращению соответствует положительная часть оси времени, а дисконтированию – отрицательная. Множитель приведения тогда можно записать в виде
Зависимость этого множителя от времени, определяемая формулой (1.3.4), приведена на рис. 1.3.1 для учетной ставки 30% годовых. Исходя из формул (1.1.7) и (1.3.4), нетрудно определить связь между процентной и учетной ставками за период Т:
Из этого соотношения следуют формулы, выражающие процентную ставку через учетную за период Т и наоборот:
(1.3.6)
(1.3.7) Если продолжительность периода равна одному году, то
Сложная учетная ставка
В случае, когда величина дисконта становится сравнимой с величиной суммы, подлежащей возврату, обычно применяют сложную учетную ставку. Процесс вычисления дисконта по сложной учетной ставке аналогичен процессу начисления сложных процентов – там производится ступенчатое начисление процентов несколько раз в течение срока кредитного соглашения, а здесь несколько раз производится ступенчатое дисконтирование суммы, подлежащей возврату. Разница заключается в направленности процессов во времени: начислению процентов соответствует прямой ход времени, дисконтированию – обратный. Определим текущую стоимость суммы S после нескольких периодов дисконтирования. В пределах одного периода производится дисконтирование по простой учетной ставке, затем полученное значение текущей стоимости суммы становится исходным для следующего периода дисконтирования и т.д. Текущая стоимость дисконтированной на один период конечной суммы равна S1=S(1-dT), в конце второго периода дисконтирования имеем S2 =S(1-dT)2 и т.д. Таким образом, после п периодов дисконтирования текущая стоимость суммы S будет равна:
Учет процентов несколько раз в год по сложной учетной ставке Если дисконтирование по сложной учетной ставке производится т раз в год, то учетная ставка за период равнаd1/m=d/m. Тогда текущая стоимость дисконтированной на 1 год конечной суммы будет равна:
где n=(1-dlm)m – годовой дисконтный множитель. Отсюда видно, что при постоянной номинальной годовой учетной ставке d конечный результат дисконтирования зависит от числа периодов в году; при одинаковой номинальной учетной ставке с увеличением количества периодов годовой дисконтный множитель уменьшается. По этой причине номинальная годовая учетная ставка не может служить универсальным измерителем эффективности финансовых операций. Реальная их эффективность связана с эффективной годовой учетной ставкой, равной относительному дисконту за год:
Доходность двух финансовых контрактов считается одинаковой, если соответствующие им эффективные учетные ставки совпадают. Номинальная годовая учетная ставка для контракта с начислением т раз в год, эквивалентная ставкеde, определяется формулой
Связь номинальной учетной ставки с номинальной процентной ставкой легко получить из формул (1.3.12) и (1.2.3 – 1.2.4):
Отсюда видно, что при т®¥, т.е. при переходе к непрерывному дисконтированию, d(m)®d, что и следовало ожидать: когда процентный доход поступает непрерывно, различие между авансовым и задолженным процентным доходом исчезает. |
||
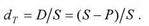 (1.3.1)
(1.3.1)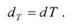 (1.3.2)
(1.3.2)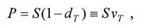 (1.3.3)
(1.3.3)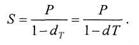 (1.3.4)
(1.3.4)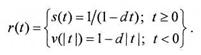 (1.3.4, а)
(1.3.4, а)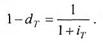 (1.3.5)
(1.3.5)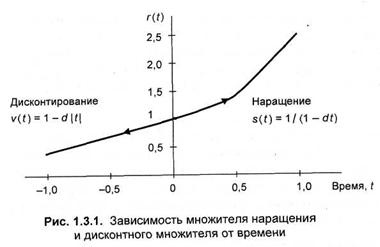
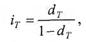
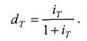
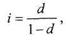 (1.3.8)
(1.3.8)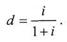 (1.3.9)
(1.3.9)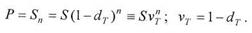 (1.3.10)
(1.3.10)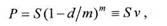 (1.3.11)
(1.3.11)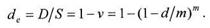 (1.3.12)
(1.3.12)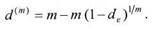 (1.3.13)
(1.3.13)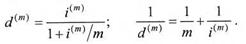 (1.3.14)
(1.3.14)