«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Финансовые и коммерческие расчеты на ЭВМ Конспект лекций.Таганрог: Изд-во ТРТУ, 2005 1.ТЕОРИЯ ПРОЦЕНТОВ 1.6. Реальная ставка доходности с учетом инфляции и налогообложения
Инфляция — это снижение реальной покупательной способности денег. В чисто финансовых расчетах, где фигурируют только изменения номинальных денежных сумм, этот фактор не учитывается. В реальности далеко не всякая ставка доходности может привлечь внимание инвесторов. Очевидно, что при темпе инфляции 50% в год едва ли кто будет вкладывать деньги под меньший процент. Такое интуитивное понимание ситуации следует дополнить количественным анализом, призванным ответить на вопрос: какова же реальная доходность инвестиций с учетом темпов инфляции? Прежде всего, необходимо ввести измеритель уровня и темпов инфляции. Стоимость инвестиций и уровня доходов разных лет может быть сопоставима только в том случае, если стоимость денежной единицы не изменяется. Уровень инфляции выражается в виде индекса цен. Индекс цен является измерителем соотношения между совокупной ценой определенного набора товаров и услуг, называемых "рыночной корзиной", для данного временного периода и совокупной ценой идентичной либо сходной группы товаров и услуг в базовом периоде:
федеральное правительство США рассчитывает индексы различных наборов, или "корзин", товаров и услуг. Наиболее известный из них — индекс потребительских цен (ИПЦ) — цена фиксированной корзины, содержащей 300 потребительских товаров и услуг, покупаемых типичным горожанином. Индекс цен валового национального продукта, или дефлятор ВНП, включает не только цены потребительских товаров и услуг, но также и цены инвестиционных товаров, товаров, покупаемых правительством, а также товаров и услуг, купленных и проданных на мировом рынке. В зависимости от характера задачи используется тот или иной индекс цен. Темпом инфляции за определенный период Т называют относительное изменение индекса цен за этот период
где Jр (0), Jр (Т) — индексы цен в начале и в конце периода. Если известны индекс цен в начале периода и прогнозируемый темп инфляции за период, то можно вычислить ожидаемый индекс цен в конце периода:
Полученное значение индекса цен будет исходным для вычислений в следующем периоде:
По прошествии т периодов индекс цен будет равен
Темп инфляции за этот интервал времени в соответствии (1.5.2) равен
Из формулы (1.5.5) видно, что возрастание индекса цен аналогично наращению денежных сумм по закону сложных процентов. Если известен темп инфляции за какую-либо l/m-ю часть года, то годовой темп инфляции в соответствии с (1.5.6) определяется формулой
Реальная ставка доходности и инфляционная премия
Инфляционное обесценение денег существенно снижает реальную доходность финансовой операции. Под реальной доходностью финансовой операции мы понимаем относительное приращение за период Т реальной покупательной способности С денежной суммы, равной отношению этой суммы к индексу цен в данный момент времени:
где S(t) — денежная сумма в момент времени t. Покупательная способность наращенной за период суммы Р равна
Подставляя это выражение в (1.5.8), получим формулу, выражающую реальную доходность через процентную ставку и темп инфляции:
Если период Т равен одному году, то нижний индекс у переменных опускают: h — годовой темп инфляции, r -реальная годовая ставка доходности. Формула (1.5.9) опровергает распространенное заблуждение, что будто бы для получения реальной ставки доходности достаточно из процентной ставки вычесть темп инфляции; это справедливо только при очень малой величине темпа инфляции, когда величиной h в знаменателе можно пренебречь по сравнению с единицей.
Формула (1.5.9) удобна для демонстрации снижения доходности инвестиций в условиях инфляции, показывающей вели чину реальной доходности при заданной процентной ставке. На практике же обычно задаются минимальной приемлемой для инвестора величиной реальной доходности (барьерной ставкой) r, исходя из которой определяют минимальную процентную ставку i, под которую еще имеет смысл инвестировать средства:
Формула (1.5.10) носит название формулы Фишера. Вторе слагаемое в правой части этой формулы – величина, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина носит название инфляционной премии. Пусть барьерная ставка равна 15% годовых при темпе инфляции, определенном в примере 1.5.2 тогда приемлемая величина процентной ставки будет равна 0,15+0,426х(1+0,15)=0,64 (64%). Из примера 1.5.2 видно, что реальная ставка доходности почти в 5 раз ниже годовой процентной ставки – впечатляющий результат! Реальная ставка доходности с учетом налога Вопрос о налогообложении прибыли от инвестирования средств приобретает особую важность, ведь налог начисляется не с реального дохода, а с номинального, равного приращению денежной суммы, и величина налога может оказаться больше реального дохода! Пусть ставка налога на прибыль равна g тогда чистая прибыль, т.е. прибыль после уплаты налога, равна iP-iPg=Pi(1-g). Отсюда видно, что учет налога на прибыль сводится к замене процентной ставки i на ставку ig=i/(l-g). Формула для реальной доходности с учетом налога на прибыль примет вид
Определим приемлемую процентную ставку с учетом налогообложения, преобразуя формулу (1.5.11):
|
||
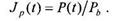 (1.5.1)
(1.5.1)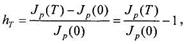 (1.5.2)
(1.5.2)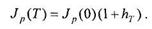 (1.5.3)
(1.5.3)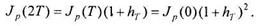 (1.5.4)
(1.5.4)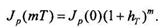 (1.5.5)
(1.5.5)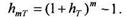 (1.5.6)
(1.5.6)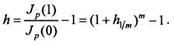 (1.5.7)
(1.5.7)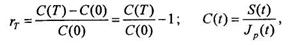 (1.5.8)
(1.5.8)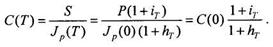
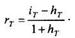 (1.5.9)
(1.5.9)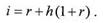 (1.5.10)
(1.5.10)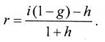 (1.5.11)
(1.5.11)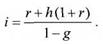 (1.5.12)
(1.5.12)