«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
Финансовые и коммерческие расчеты на ЭВМ Конспект лекций.Таганрог: Изд-во ТРТУ, 2005 2. ОЦЕНКА И АНАЛИЗ ДЕНЕЖНЫХ ПОТОКОВ 2.2. Простые проценты
Часто в течение срока действия кредитного соглашения сумма задолженности уменьшается за счет частичного погашения задолженности или, наоборот, возрастает при дополнительном заимствовании средств. В этом случае проценты начисляются отдельно за каждый период, в течение которого сумма задолженности постоянна, а затем начисленные для отдельных периодов времени проценты суммируются. Расчет производится по формуле простых процентов
где Р — сумма на счете; i — номинальная годовая процентная ставка;
Суммарную величину процентов можно получить, если просуммировать проценты, начисленные на каждый платеж с момента, когда он внесен, и до момента начисления t (окончания срока):
где tk — момент внесения k-го платежа в размере Rk. Тогда сумма, которую получит клиент при закрытии счета, равна
Очевидно, эта величина и есть накопленная сумма (стоимость) фонда при начислении простых процентов. Динамика изменения накопленной стоимости для примера 2.1.1 приведена на рис. 2.1.1.
Постоянная рента
Наиболее простой пример потока платежей — финансовая рента. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой или аннуитетом (от annuity — ежегодный) вне зависимости от происхождения этих платежей, их назначения и целей. Интервал времени между двумя последовательными платежами называют периодом ренты.
По величине членов ренты делятся на постоянные (с равными членами) и переменные. Очень важно различие рент по моменту выплаты платежей. Если платежи осуществляются в конце определенного периода времени (месяца, квартала, года и т. п.), как это обычно и бывает, то такие ренты называются обычными или постнумерандо (ordinary annuity).Если же выплата производится в начале каждого периода, то соответствующие ренты называют приведенными илипренумерандо (annuity due). По вероятности выплаты отдельного платежа ренты делятся на верные и условные. Верные ренты подлежат безусловной выплате, например при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. К такого рода рентам относятся страховые ренты, в частности выплаты пенсии, которые производятся при условии, что получатель ее дожил до срока очередной выплаты. Для постоянной ренты пренумерандо сумма начисленных процентов определяется формулой (2.1.1), где все платежи равны между собой, количество платежей – п, период ренты – Т. Проводя суммирование по формуле арифметической прогрессии, получим сумму процентов и накопленную сумму:
где R – сумма платежа; FV – накопленная (наращенная) сумма. Определим теперь текущую стоимость PV ренты пренумерандо, дисконтируя наращенную стоимость на срок ренты:
Для постоянной ренты постнумерандо сумма начисленных процентов также определяется формулой (2.1.1), где все платежи равны между собой и равны R, количество платежей равно и, период ренты равен T, но уплата первого платежа – в момент времени t=Т. В результате получаем
Погашение задолженности
Еще одна важная сфера применения простых процентов — расчет платежей при погашении кредита частями (в рассрочку). Часто условиями кредитного договора предусмотрено погашение долга не разовым платежом, а несколькими платежами в течение оговоренного срока. При этом условиями договора задается динамика погашения основного долга, а проценты за каждый период времени начисляются на невыплаченный остаток основного долга (т. е. сумму задолженности). Каждая выплата состоит из части основной суммы долга и указанных выше процентов. Если в какой-то момент времени заемщик решит досрочно погасить долг, то он должен выплатить сумму текущей задолженности, т. е. остаток основного долга и проценты, начисленные на этот остаток с момента последней выплаты. Динамика изменения текущей задолженности для примера 2.1.3 показана на рис. 2.1.2. Метод погашения основной суммы долга равными частями — наиболее простой и широко распространенный. Получим общую формулу для величины очередной выплаты, включающей погашение части основного долга и проценты с задолженности. Если сумма кредита равна D, срок кредита равен и лет, кредит погашается равными частями, выплачиваемыми в конце каждого года, то размер выплаты в конце каждого года, состоящей из погашаемой части основного долга и процентов с суммы задолженности, составляет R
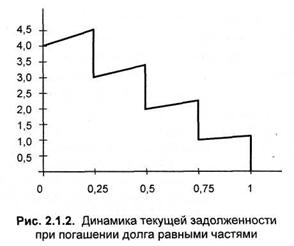
Соответственно задолженность на начало к-го года равна D-D(k-1)/n, проценты за к-й год равны iD[l-(к-1)/п], выплата в конце к-го года
Последняя выплата при полном погашении кредита равна
В случае если погашение долга производится чаще, чем раз в год (т раз в год), то за каждую выплату будет погашаться 1/тп часть долга, а проценты будут начисляться каждый раз не за год, а за 1/т-ю часть года. Формулу дляк-й очередной выплаты (к – порядковый номер выплаты, а не номер года выплаты, как выше!) легко получить из (2.1.7), заменяя в ней i на i/m, п на пт:
В современной практике часто используется также метод погашения кредита равными срочными выплатами, включающими погашение основной части долга переменными суммами и выплату соответствующей части процентов. При этом величина очередной части погашения основного долга подбирается таким образом, чтобы величина всех очередных выплат была одинаковой. Поскольку величина очередной суммы погашения основного долга зависит от ставки процентов и при этом теряется простота метода простых процентов, логичнее этот метод погашения долга рассматривать в разделе сложных процентов. |
||
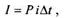 (2.1.1)
(2.1.1) t — продолжительность периода, за который рассчитываются проценты.
t — продолжительность периода, за который рассчитываются проценты.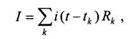 (2.1.2)
(2.1.2)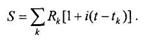 (2.1.3)
(2.1.3)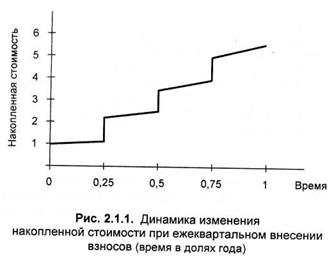
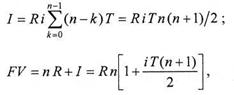 (2.1.4)
(2.1.4)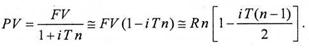 (2.1.5)
(2.1.5)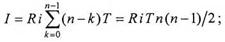
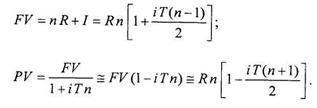 (2.1.6) - первая
(2.1.6) - первая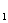 =D/n+Di. Задолженность на начало второго года равна D-D/n, проценты за второй год равны iD (1-1/n), выплата в конце второго года
=D/n+Di. Задолженность на начало второго года равна D-D/n, проценты за второй год равны iD (1-1/n), выплата в конце второго года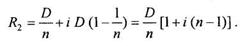
 (2.1.7)
(2.1.7)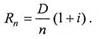 (2.1.8)
(2.1.8)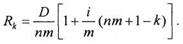 (2.1.9)
(2.1.9)