«Управление и Оптимизация Производственного Предприятия»
|
|
|
|
|
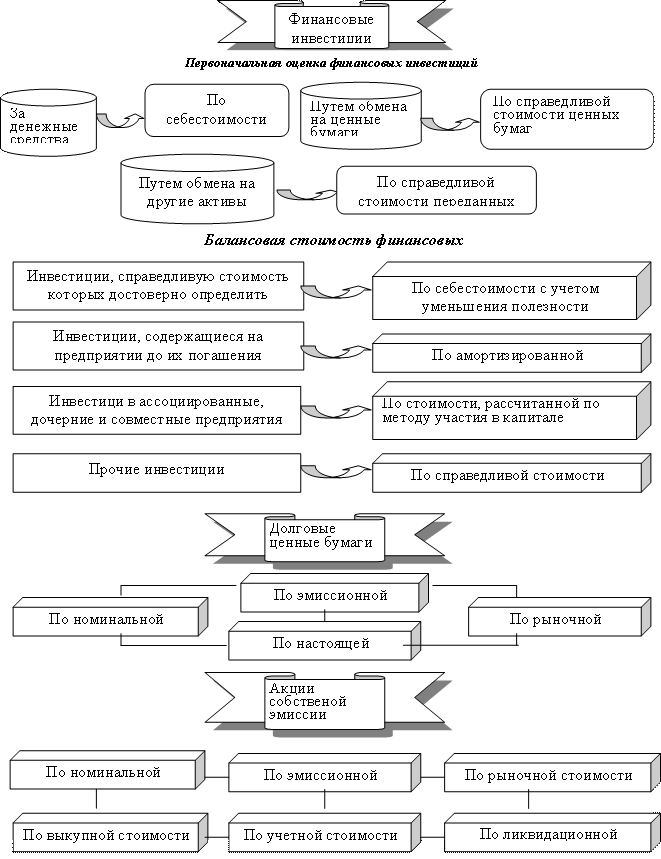
Корпоративные ценные бумаги как инструмент инвестиционной привлекательности компаний Под ред. д.э.н., профессора А.Н. Асаула. – СПб: АНО «ИПЭВ», 2008. -288с. Глава 2. Корпоративные ценные бумаги 2.2. Акции – основной источник собственного капитала акционерного общества 2.2.3. Модели оценки акций. Оценка ценных бумаг собственной эмиссии, воплощенных в собственном капитале, в частности, в авансированной его части, не влияет на оценку собственного капитала в целом. В то же время ценные бумаги, а именно акции собственной эмиссии, для нужд бухгалтерского учета должны быть оценены по номинальной, рыночной, эмиссионной, выкупной, учетной (балансовой) и ликвидационной стоимости. На рис. 2.19 представлены определенные системой учета способы оценки ценных бумаг.
Рис. 2.19. Способы оценки ценных бумаг Оплата акций общества при его основании проводится по их номинальной стоимости. Во время всех последующих выпусков реализация акций осуществляется по эмиссионной цене. Это обусловливается тем, что собственный капитал акционерного общества выше уставного, поскольку в процессе существования акционерного общества происходит увеличение стоимости его активов вследствие инфляционных процессов, присоединения нераспределенной прибыли и т. п. Специфика акций состоит в том, что для них вводятся несколько категорий стоимостей, из которых можно выделить: рыночную стоимость, экономическую стоимость, номинальную стоимость, балансовую стоимость, эмиссионную стоимость, ликвидационную стоимость. Рыночная стоимость определяется в каждый текущий момент действующей рыночной ценой акции. Если эту цену умножить на количество находящихся в обращении акций, то получится рыночная стоимость собственных средств корпорации. Экономическая стоимость акции представляет собой приведенную стоимость тех потоков денег, которые в данный момент инвестор ожидает получить от акции в будущем. Иными словами, это дисконтированная стоимость будущего потока дивидендов и цены акции в момент ее продажи (акция обеспечивает только эти два вида денежных потоков). Номинальная стоимость Рномин. – это та официальная цена акции, которая устанавливается создателями акционерного общества в момент утверждения его устава; это доля уставного капитала, приходящаяся на одну акцию. Номинальная стоимость определяет минимальную стоимость акции, которая не может быть снижена путем выплаты дивидендов, это тот минимум, который могут получить владельцы акций в случае ликвидации АО. В связи с этим номинальная стоимость акций устанавливается обычно очень низкой. Если умножить величину номинальной стоимости обыкновенной акции Рномин на количество находящихся в обращении акций данного эмитента (положим, «Салюта») N, то получим величину уставного капитала «Салюта» = N Когда происходит первичное размещение дополнительных акдий, то устанавливаемая цена размещения (эмиссионная стоимость) Рразмещ. практически всегда превышает номинальную стоимость. Если было размещено дополнительно М акций «Салюта» по цене Рразмещ., то собственные средства «Салюта» возрастут на величину: М Наконец, по результатам года «Салют» может иметь чистую прибыль. Часть этой прибыли выплачивается акционерам в виде дивиденда, а оставшаяся часть – нераспределенная прибыль – реинвестируется. Накопленные суммы нераспределенной прибыли учитываются нарастающим итогом. Общая сумма уставного капитала, добавочного капитала и нераспределенной прибыли составляет собственные средства акционерного общества и учитывается в разделе «капитал плюс резервы» пассива баланса. Балансовая стоимость акции представляет собой величину, полученную делением суммы собственных средств фирмы на количество обыкновенных акций. Балансовую стоимость акций определяют во время аудиторских проверок в том случае, когда эмитент собирается пройти листинг для включения своих акций в биржевой список ценных бумаг, допущенных к биржевым торгам, а также во время ликвидации акционерного общества, чтобы определить долю собственности, приходящейся на акцию (если в составе капитала нет привилегированных акций). В ином случае определяется ликвидационная стоимостьакций. Существуют три теоретические модели оценки акций – дисконтирования потока дивидендов, дисконтирования потока доходов и дисконтирования потока денег. Если используемые в этих моделях переменные величины подобраны правильным способом, то все модели дадут один и тот же результат. Наиболее часто используется модель дисконтирования дивидендов. Модель дисконтирования дивидендов. Представим, что в исходный момент времени t=0 цена акции составляла Р0 руб. По прошествии холдингового периода цена акции возросла до Pi руб. и владельцу акции выплачивается дивиденд в размере D1 руб. Тогда доходность к акции за холдинговый период:
Эту формулу можно преобразовать и найти величину Р0:
Норму отдачи k, которая в формуле (2.5) служит ставкой дисконта для вычисления приведенной стоимости акции, называется рыночной ставкой капитализации. В условиях эффективного рынка ставка капитализации (она же в данном случае и требуемая норма отдачи) отражает издержки упущенной возможности размещения денег в акцию. Строго говоря, формула дисконтирования позволяет утверждать, что приведенная стоимость акции PV (что и определяет цену акции в исходный момент времени) может быть представлена в виде:
где: – D1,D2, D3,…,Dn – денежные потоки в момент 1,2,...,n; – k1,k2,k3,…kn – рыночные ставки капитализации в момент 1,2,...,n; – n – количество лет, в течение которых инвестор предполагает владеть акцией. Формула (2.6) предполагает, что инвестор должен задать прогнозируемые величины денежных потоков D1 и ставок дисконта k1 на «n» лет вперед, что делает задачу вычисления Р0 практически невыполнимой. Поэтому для построения приемлемой математической модели необходимо пойти на ряд существенных допущений и упрощений. 1. Будем считать, что k1=k2=...=k. Иными словами, в любой момент инвесторы всегда одинаково оценивают риск, связанный с данной акцией. Это допущение не столь жесткое, поскольку аналогичное делается и при оценке, например, реальных средств. 2. Предполагается, что любая величина Dt=Dt-1 Наиболее простая модель оценки стоимости акции предложена американским экономистом Майроном Гордоном (Myron J. Gordon) в 1962 г. Для ее построения Гордон пошел на другие упрощения: – во-первыгх, поскольку срок действия акции теоретически не ограничен, то считаем, что поток денежных выплат представляет собой бесконечный поток дивидендов (ликвидационной суммы уже не будет, так как акция существует бесконечно долго). Иными словами, с учетом уже сделанных упрощений формулу (2.7) можно представить так:
– во-вторых, Гордон предложил считать все величины g, равными друг другу, т. е. дивиденды возрастают ежегодно в (1+g) раз, причем величина g не меняется до бесконечности. Иными словами, в модели Гордона: D2-D, D3 = D2 D4 = D3 С учетом этого допущения формула (2.8) примет вид:
Если же считать, что дивиденд D1 = D0
Выражение (2.10) представляет собой бесконечно убывающую геометрическую прогрессию. Сумма членов такой прогрессии:
Итак, согласно модели Гордона приведенная стоимость акции Ро определяется делением величины ожидаемого по результатам текущего года дивиденда D1 на разность между рыночной ставкой капитализации k и ожидаемой ставкой прироста дивиденда g. Модель Гордона дает возможность быстрой оценки текущей стоимости акций, однако прежде чем применять ее и на этой основе делать инвестиционное решение, необходимо иметь в виду следующие обстоятельства: поскольку модель предполагает дисконтирование поступающих дивидендов вплоть до бесконечности, то формула (2.11) очень чувствительна даже к небольшим изменениям исходных данных. Кроме того, помимо уже упоминавшихся упрощений и дополнений модель Гордона предполагает, что: – k должно быть всегда выше g, поскольку в противном случае цена акции становится неопределенной. Это требование вполне логично, так как величина g (темпа прироста дивидендов) может в какой-то момент превысить требуемую норму отдачи акции k, но этого не может произойти, если полагать бесконечным выбранный срок дисконтирования, ибо в данном случае дивиденды постоянно прирастали бы с более высокими темпами, чем норма отдачи акции, что не может быть; – фирма должна выплачивать дивиденды регулярно. Если этого не произойдет, модель Гордона неприменима. Более того, требование неизменности величины g означает, что фирма направляет на выплату дивидендов всегда одну и ту же долю своего дохода; – требование неизменности величин k и g вплоть до бесконечности ограничивает структуру капитала фирмы: необходимо предполагать, что единственным источником финансирования фирмы являются ее собственные средства и отсутствуют иные внешние источники. Новый капитал поступает на фирму только за счет удерживаемой доли дохода, и чем выше доля дивидендов в доходе фирмы, тем ниже уровень обновления капитала. Конечно, весь набор ограничений в модели Гордона нереален, но он необходим для создания математической модели. Взаимосвязь факторов, воздействующих на стоимость акции. Обратимся к формуле (2.11):
и выразим отсюда ставку капитализации:
Первое слагаемое D1/P0 называют дивидендной доходностью, и ее оценка не вызывает особой сложности. Труднее обстоит с величиной g. Для ее оценки можно применить следующий способ: пусть в течение года акция принесла прибыль на акцию E1. Выплачиваемые дивиденды определяются долей выплат р: D1=p
Можно доказать, что величина g=b
Данная формула связывает между собой две нормы отдачи: k – ставку капитализации, определяющую издержки упущенной возможности приобретения акции, т. е. норму отдачи наилучшего альтернативного средства такого же уровня риска, и ROE – доходность капитала. Взаимодействие этих двух величин с учетом дивидендной политики фирмы (что определяется величиной воздействуют на текущую стоимость акции, и все акции условно можно разбить на три группы: акции «нормальных» компаний, акции «растущих фирм», акции «угасающих» фирм. Нормальные фирмы характеризуются тем, что для них k=ROE. Значит, нормальная фирма и ее конкуренты выбрали возможности инвестировать собственные средства в проекты с NPV>0 и вынуждены вкладывать деньги в инвестиции с NPV=0. Поэтому ROE каждой фирмы уравниваются и приближаются к рыночной ставке капитализации к. Подставим выражение k=ROE в формулу (2.9) и получим:
Эта формула позволяет сделать два вывода: во-первых, ставка дисконта может быть выражена через соотношение P0/E1 только в том случае, если k=ROE (замечание важное, поскольку величина Р/Е является одной из важных качественных характеристик акций, приводящихся в таблицах котировки акций). Попытка использовать величину, обратную отношению Р/Е, в качестве ставки дисконта в формуле Гордона может дать результат, далекий от истины, если k Для растущей фирмы ROE>k, т. е. эта фирма имеет возможность инвестировать собственные средства в такие проекты, для которых NPV>0. Иными словами, подобные фирмы имеют возможность приобретать капитальные ресурсы с издержками k процентов и получать от их эксплуатации норму отдачи ROE, превышающую k. Наконец, для угасающей фирмы ROE<k – она не в состоянии реинвестировать деньги в проекты с NPV>0. Подобные фирмы переживают значительное сокращение производства и, как правило, получают отдачу за счет более высокой доли дивиденда. Необходимость в рыночной оценке акций возникает при поглощении и слиянии общества, купле голосующего пакета акций, выдаче кредита под обеспечение акций, преобразовании ОАО в ЗАО, определении целесообразности купли раннее реализованных собственных акций, реорганизации и ликвидации общества. В практике функционирования акционерных обществ имеет место объединение компаний посредством обмена функциями. Существуют два варианта: в первом – каждая из двух компаний сохраняется в неизменном виде, но происходит взаимный обмен акциями, таким образом, каждая компания владеет определенным количеством акций другой компании и ряд директоров входят в советы директоров обеих компаний. Во втором варианте происходит слияние двух компаний и акции одной компании обмениваются на акции другой компании. Обмен может происходить с доплатой или 1:1. С рыночной стоимостью, как правило, совпадает выкупная стоимость акций, кроме случаев, когда акционерное общество реорганизуется. В заключение необходимо подчеркнуть, что главная экономическая и финансовая цель акционерного общества – это обеспечение благосостояния акционеров. При этом одни компании стремятся продемонстрировать динамичный рост прибыли и стоимости акций, а другие стараются стабильно выплачивать высокие дивиденды. В России сложилась особенная ситуация, когда возможно и то и другое одновременно. |
||
 Pномин.
Pномин.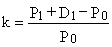 (2.4)
(2.4)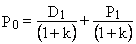 (2.5)
(2.5)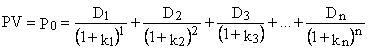 (2.6)
(2.6)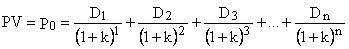 (2.7)
(2.7)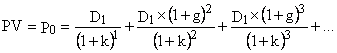 (2.8)
(2.8)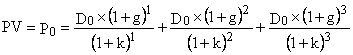 (2.9)
(2.9)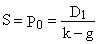 (2.10)
(2.10)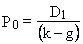 (2.11)
(2.11)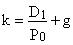 (2.12)
(2.12)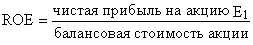
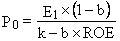 (2.13)
(2.13)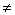 ROE). Во-вторых, если фирма «нормальная», то инвесторам абсолютно безразлична ее дивидендная политика – они получают одинаковую отдачу от акции вне зависимости от соотношения дивидендов и ценового выигрыша.
ROE). Во-вторых, если фирма «нормальная», то инвесторам абсолютно безразлична ее дивидендная политика – они получают одинаковую отдачу от акции вне зависимости от соотношения дивидендов и ценового выигрыша.